A state-resonant energy transmission law for energy materials and beyond

Energy materials research has achieved remarkable progress in materials discovery and device performance, yet a minimal and unified physical description of energy transport remains lacking. Existing transport models are often phenomenological and restricted to specific carriers or regimes, limiting their ability to bridge classical and confined quantum transport.

In materials science, energy transport is commonly described by phenomenological laws: Ohm’s law for electrons, Fickian diffusion for ions, or hopping models for polarons and ion motion^[1,2]. While successful within their respective regimes, these descriptions remain phenomenological and do not explicitly address how energy-state accessibility governs transport across classical and confined regimes. More importantly, they implicitly assume that transport is governed by particle migration, with flux determined by scattering, diffusion, dissipation, and local equilibrium.

Recent advances in quantum materials and nanoscale architectures challenge this view. Transport increasingly appears to be governed not by migration probability but by energy-state accessibility, coherence, and field-geometry coupling. This observation calls for a minimal, physically transparent energy transmission law that complements existing energy relations.

We propose the state-resonant energy transmission law (SRETL), a minimal transmission law at the phenomenological level, analogous in status to Ohm’s law or Fick’s law,

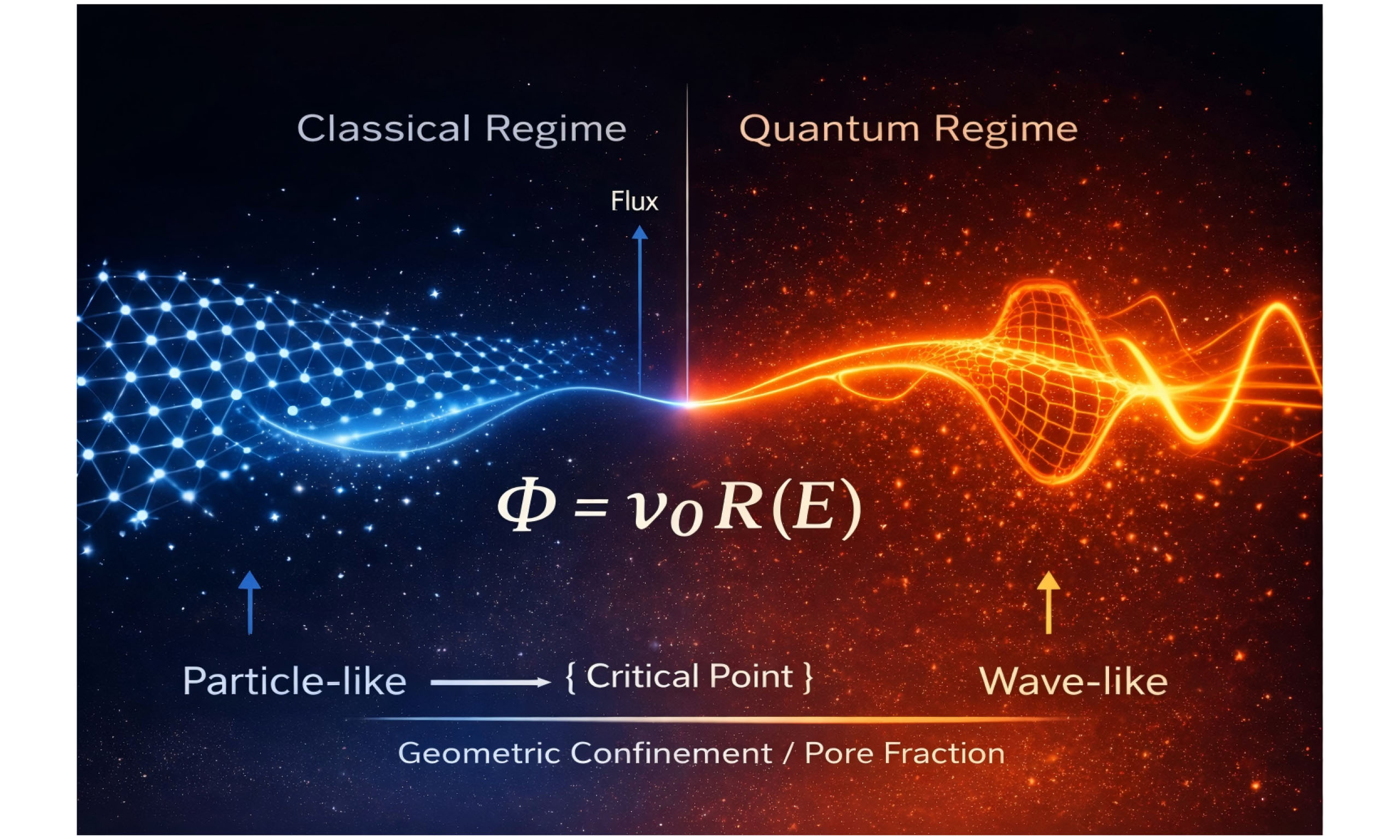
where Φ is the macroscopic energy flux, ν₀ is an intrinsic activation frequency, and R(E) is an energy-dependent transmission function. This equation provides a fundamental statement of transmissibility, identifying wave-particle duality as a manifestation of transmission-law selection: when R(E) is broad and scattering-dominated, carriers behave as particles (classical migration), whereas when R(E) is resonant and field-confined, carriers behave as coherent waves (quantum transmission).

This formulation is deliberately minimal: it does not assume specific carriers, scattering mechanisms, or transport pathways. Instead, it asserts that transport is primarily governed by the accessibility of allowed energy states, shaped by geometry, fields, and boundary conditions.

This law may open a new era of energy materials research by shifting the focus from reducing resistance to engineering state accessibility for protons and ions. As an example, in charge transport involving electrons and ions in the classical limit, where energy states are densely distributed and scattering dominates, the transmission function R(E) varies smoothly with energy. and in the classical dissipation-limited limit, the energy transmission flux Φ reduces to the conventional current density J^[1,2],

where J is the current density, σ is the conductivity, and E is the applied electric field, corresponding to dissipation-limited transport with well-defined resistance.

In contrast, when confinement, fields, or interfaces restructure the energy landscape, R(E) becomes sharply energy-selective. Transport then proceeds via resonant state transmission, yielding non-classical behavior and abrupt flux enhancement.

Within the SRETL framework, wave-particle duality in ionic systems, particularly for protons, is no longer treated as an intrinsic ambiguity of the carriers but as a direct consequence of the governing energy transmission regime. This formulation transcends the conventional ion-transport paradigm, in which transport is assumed to be universally migration-limited and particle-like. Instead, the SRETL establishes that classical migration and wave-like, resonance-mediated transmission are complementary limits of a single governing law, with the operative behavior determined by energy-state accessibility, phase coherence, and interference imposed by geometry and field confinement. As a result, ionic transport is redefined from a purely kinetic process to a state-governed energy transmission phenomenon.

This insight breaks the long-standing conceptual constraints of ionics imposed by purely structural and migration-based frameworks and establishes a new paradigm for understanding ionic transport^[3,4]. In this view, ions, particularly protons, are no longer merely diffusing particles but carriers of energy transmission that can be coherently structured, selectively activated, and amplified through material design. When energy-state accessibility is smooth and dense, transport appears particle-like and migration-limited; when accessibility becomes selective and resonant, transmission acquires wave-like, state-mediated characteristics. This reinterpretation is fully consistent with quantum mechanics and reflects the governing transport regime rather than the microscopic nature of the particles. Within this redefined picture of ionic transport, the SRETL naturally motivates a Quantum Ionics framework: a systematic language for describing ionic transmission in terms of energy states, coherence, and resonance, extending beyond traditional structure-migration descriptions.

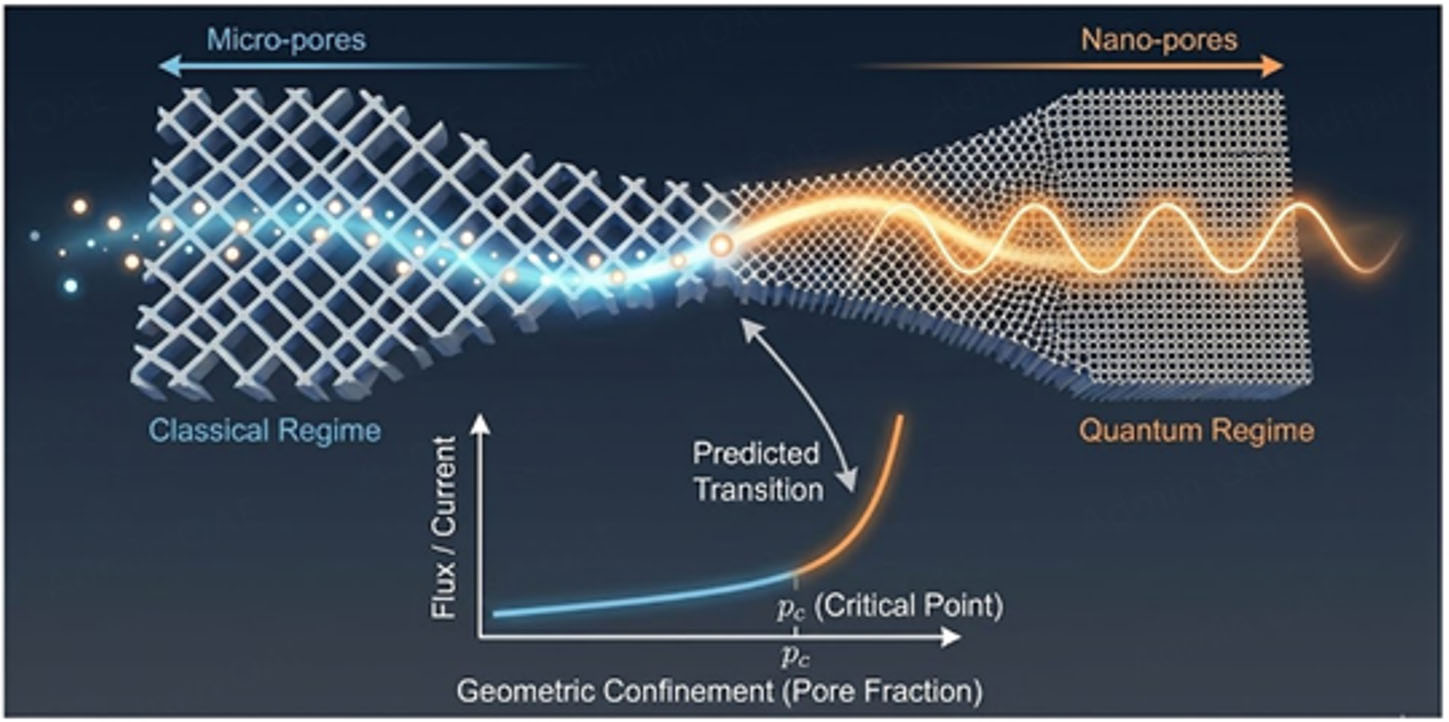
Rather than relying on specific materials or devices, this theory predicts a generic geometric verification principle and a new material design paradigm. Hierarchical nano-micro architectures provide a natural platform for this purpose [Figure 1]. In such structures, classical and quantum transport coexist: weakly confined micro-scale regions support migration-limited transport, while strongly confined nano-scale regions promote state-mediated transmission. In these systems, a critical point p_c emerges: as geometric confinement is increased via pore fraction, interface density, or characteristic length scales, a sharp transition occurs at p_c, marking the onset of a state-governed transport/transmission regime.

Figure 1. Probing the critical transition in hierarchical frameworks. In this figure, p_c denotes a geometric threshold at which state accessibility becomes resonant-dominated. Note: This figure is schematic and intended to illustrate structural relations at the law level, rather than detailed geometries or specific material implementations.

Crucially, as shown in Figure 1, the theory predicts that modifying geometric confinement, including the associated field confinement, shifts the position of a critical point, p_c. Narrower confinement distributions yield sharper transitions. The transition remains observable even when classical transport persists in parallel. These predictions provide a direct experimental route to test the minimal energy transmission law without invoking specific materials or carrier species.

Extracting a state-resonant transmission function from ultrafast phase-delay measurements

Recent advances in quantum materials and nanoscale architectures challenge purely migration-based views of transport. A typical example is found in a recent study on quantum materials^[5], which demonstrates that phonon-driven modulation of electronic localization reshapes local field effects (LFEs), producing absorption changes that cannot be explained by state filling or Pauli blocking alone. The coherent A_1g phonon periodically alters internal electric fields and orbital localization, dynamically sculpting the local energy landscape experienced by carriers. This behavior motivates a reinterpretation of phonons not primarily as dissipative baths, but as dynamic gates that transiently enable or suppress transitions. Throughout this work, the term transmission is used deliberately to distinguish state-resonant energy flow from conventional particle-migration-based transport.

Within this framework, we propose that the observed dynamics are governed by a state-resonant energy transmission principle, expressed by Eq. (1), where Φ denotes the carrier flux or transition rate, ν₀ is an intrinsic attempt frequency set by lattice or local-field oscillations, and R(E) is an energy-selective transition probability determined by the instantaneous local energy landscape. Here, the relation is introduced as a phenomenological invariant inferred from experimental observables, rather than as a microscopic derivation.

According to this principle, carriers do not respond continuously to lattice displacement. Instead, they remain in metastable configurations until lattice motion and LFEs jointly minimize the effective transition energy, at which point a resonance-enabled transition occurs. The experimentally measured phase delay thus reflects a waiting time for minimal-energy alignment, rather than a relaxation timescale in the conventional sense^[6]. Strong electron-phonon coupling (EPC) enhances the amplitude of energy-landscape modulation and therefore increases R(E), but the timing of the transition is governed by the resonance condition itself. LFEs provide spatial confinement and orbital selectivity, sharpening this condition and enabling site-resolved dynamics.

Reinterpreting the results of Neb et al. within this energy-resonance framework unifies several key observables:^[5]

• Phase shifts (Δφ) directly map waiting times for state resonance-energy alignment.

• EPC strength (λ) controls the amplitude of energy-landscape modulation, determining how effectively the gate opens.

• LFEs provide spatial confinement and orbital selectivity that sharpen resonance conditions.

Within the SRETL framework, the experimentally observed phase delay Δϕ(E) is interpreted as the waiting time required for the energy landscape to reach a resonant transmission condition. The effective transmission function R(E) is thus temporally modulated by coherent phonon motion and LFEs, rather than being continuously sampled. If the phonon amplitude is reduced below a critical threshold, Δϕ increases sharply while Φ collapses discontinuously, reflecting the inability to reach the resonance condition, even though EPC remains finite. The SRETL predicts that analogous phase-gated resonance transmission should occur for ionic and protonic carriers in confined oxides, where lattice vibrations and local electric fields modulate state accessibility rather than scattering rates.

The implications extend beyond MXenes or electronic carriers. Any system in which transport occurs through a dynamically modulated energy landscape, including proton conduction in confined oxides, mixed electron-ion conductors, and electrochemical interfaces, may operate under analogous minimal-energy resonance constraints. From this standpoint, nonadiabatic transport is not inherently stochastic but can, in principle, be engineered by controlling local fields exhibiting LFEs, phonon modes, or structural motifs that define when resonance conditions are met.

The attosecond-resolved measurements reported by Neb et al.^[5] provide an experimental realization of the minimal-energy resonance condition implicit in the SRETL. Rather than interpreting the observed phase delays solely as nonadiabatic relaxation times, the SRETL framework reinterprets them as waiting times for state-resonant transmission. This distinction is not semantic: it implies that carrier motion is gated by discrete resonance conditions rather than continuously driven by lattice motion. As a result, the experimentally observed dynamics encode a transmission function R(E) that can, in principle, be reconstructed from phase-delay (Δϕ) and EPC amplitude (λ) measurements, as illustrated in Figure 2.

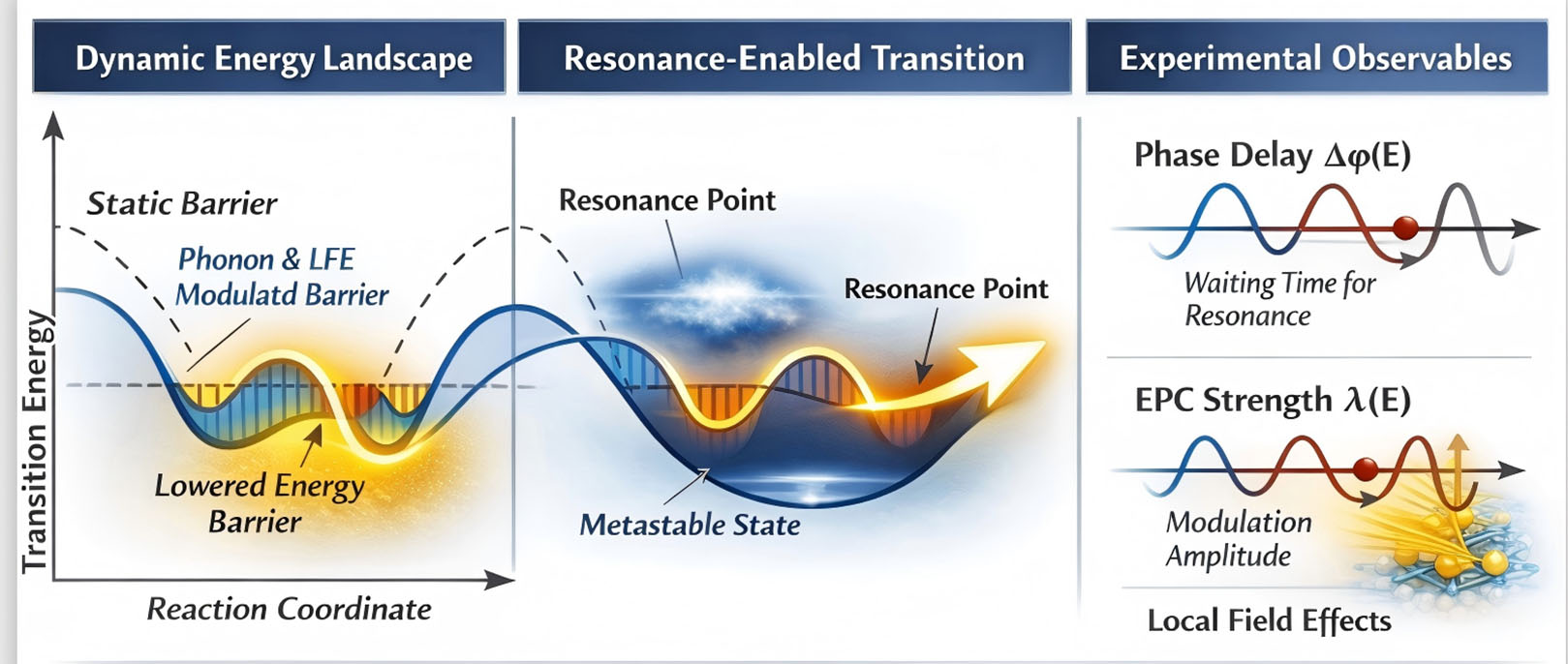
Figure 2. Minimal-energy resonance governs ultrafast carrier-lattice dynamics. Schematic illustration of the minimal-energy resonance transition principle underlying nonadiabatic carrier transport. Left: Coherent lattice motion and local field effects (LFEs) dynamically modulate the effective energy landscape, periodically lowering transition barriers relative to the static configuration. Center: Carriers remain trapped in metastable states and undergo transition only when lattice displacement and LFEs jointly satisfy a minimal-energy resonance condition, leading to a discrete, resonance-enabled transition rather than continuous adiabatic following. Right: Experimental observables associated with this process: the energy-dependent phase delay Δφ(E) reflects the waiting time for resonance alignment; the electron-phonon coupling strength λ(E) controls the amplitude of energy-landscape modulation; and LFEs provide spatial confinement and orbital selectivity that sharpen the resonance condition. Together, these elements establish minimal-energy resonance as the governing principle of ultrafast carrier-lattice dynamics beyond relaxation-limited or adiabatic descriptions.

Outlook: toward a unified energetic description

To arrive at a truly fundamental understanding of the energy materials we engineer, we must transcend empirical approximations and revisit the ontological roots of physics itself. The intrinsic nature of energy and matter and the profound unity between them are rigorously codified by Albert Einstein’s three foundational relations, here in this work referred as Harmonic Trio.

These relations define what energy is and how it exists, but they do not by themselves prescribe how energy is dynamically transmitted through structured materials^[7-9]. Yet, despite their profundity, these relations do not explicitly address how energy is transmitted dynamically through structured material systems, particularly under non-equilibrium, confined, and quantum-enabled conditions relevant to modern energy materials. Herein, the SRETL emerges from state-selective activation, resonance-mediated coupling, and field-confined energy-state evolution, processes that are implicitly allowed by the Harmonic Trio but not governed by it. This conceptual gap, between the definition of energy and its dynamic transmissibility, becomes decisive in advanced electrochemical and solid-state energy systems.

The framework presented here is motivated by conceptual consistency with the spirit of Einstein’s unified field program^[7-9], while remaining firmly at the level of energy transmission rather than fundamental interactions. Stimulated by the Harmonic Trio, we further note that the missing piece is not an additional “existence equation,” but a dynamic law of transmission, expressed as:

At the level of definition and constraint, energy is characterized by mass equivalence, quantization, and coupling to geometry. At the level of transport, a separate closure is required to connect energy-state accessibility to the observable flux. The SRETL provides this closure in its minimal form: Φ = ν₀R(E), thus leading to a harmonic Quartet.

Einstein’s relations articulate how energy is defined (mass-energy equivalence), quantized (frequency-energy relation), and constrained by geometry (energy-momentum sourcing curvature). These cornerstones clarify what energy is, but they do not by themselves provide an operational closure for how energy becomes an observable flux in structured, non-equilibrium material systems. The SRETL is introduced precisely at this transmission layer: it links the accessibility of energy states, shaped by fields, interfaces, and confinement, to a measurable transmission rate or flux.

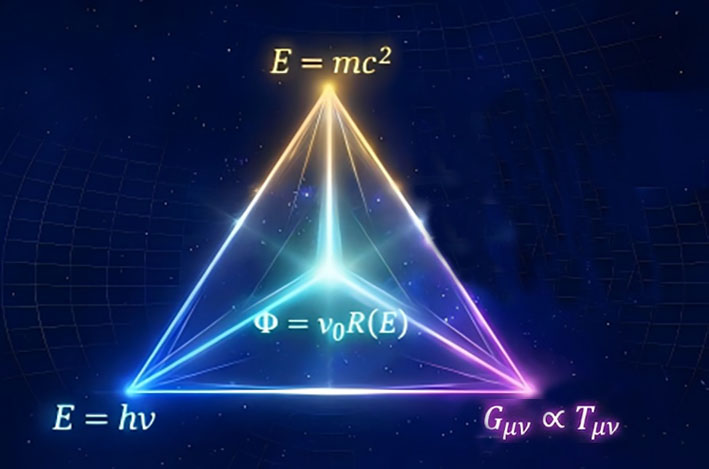
When considered alongside Einstein’s three foundational relations, the SRETL completes a conceptually coherent set of energy descriptions. Within this quartet, the static existence of energy and matter is complemented by an explicit description of dynamic energy transmission. Rather than treating gravity (geometry), quantum mechanics (frequency), and transmission (flux) as separate domains, this framework highlights them as coupled expressions of a single physical reality viewed from different descriptive levels. The SRETL introduced here complements this framework by focusing on energy transmission at the level of transmission. In this view, the four relations together form a harmonic set of energy descriptions, as illustrated in Figure 3, in which substance, state, geometry, and flow are treated as distinct but mutually consistent aspects of energy-material physics.

Figure 3. The conceptual descriptor set of energy and matter and a three-dimensional extension of Einstein’s energy relations enabled by the SRETL. The fundamental nature of our universe is defined by three static pillars, now complemented by the minimal energy transmission law. The SRETL is positioned at the center as a transmission-level relation that connects substance, state, geometry, and flow. This unified framework suggests that transport in energy materials is not merely particle migration, but can be viewed as a conceptual descriptor set describing energy. It highlights how energy transmission constitutes an additional, orthogonal dimension in the description of physical systems, complementing existing energetic relations and enabling a more complete perspective on energy behavior across material and cosmological contexts. (Note: This figure is schematic and intended to illustrate structural relations at the law level, rather than detailed geometries or specific material implementations. Here we place the SRETL within a broader physical context, showing that it complements Einstein’s foundational relations by introducing flux as an independent descriptor. This conceptual descriptor set provides a coherent description of energy from microscopic state transmission to macroscopic transport, without invoking a unified field theory).

This construction does not constitute a unified field theory, nor does it invoke new fundamental interactions. Instead, it introduces a transport-level perspective that is conceptually consistent with the unifying spirit of Einstein’s program, while remaining firmly grounded in experimentally accessible energy materials and transmission phenomena. In this sense, the SRETL provides a previously under-articulated dynamical connection between energy as a physical entity in matter and energy as an observable flux. Further theoretical extensions toward deeper formal unification are intentionally left for future work.

This perspective naturally unifies transport phenomena across energy materials and emerging quantum-enabled energy platforms, providing a physically grounded pathway for bridging classical and quantum regimes within practical materials. Classical transport laws emerge naturally as limiting cases when energy-state accessibility is smooth and scattering-dominated. When confinement and fields restructure the energy landscape, energy transmission becomes state-mediated, giving rise to non-classical and quantum-like transmission behavior. More broadly, it suggests that transmission should be viewed not as an auxiliary phenomenon, but as a basic form of expression through which energy is structured, accessed, and transmitted in physical systems. In this sense, the SRETL offers a transport-level complement to existing energetic frameworks, informing future efforts toward a more unified understanding of energy in motion.