A critical review of machine learning interatomic potentials and Hamiltonian
Abstract
Machine learning interatomic potentials (ML-IAPs) and machine learning Hamiltonian (ML-Ham) have revolutionized atomistic and electronic structure simulations by offering near ab initio accuracy across extended time and length scales. In this Review, we summarize recent progress in these two fields, with emphasis on algorithmic and architectural innovations, geometric equivariance, data efficiency strategies, model-data co-design, and interpretable AI techniques. In addition, we discuss key challenges, including data fidelity, model generalizability, computational scalability, and explainability. Finally, we outline promising future directions, such as active learning, multi-fidelity frameworks, scalable message-passing architectures, and methods for enhancing interpretability, which is particularly crucial for the field of AI for Science (AI4S). The integration of these advances is expected to accelerate materials discovery and provide deeper mechanistic insights into complex material and physical systems.
Keywords
INTRODUCTION
Density functional theory (DFT) and molecular dynamics (MD) underpin modern computational materials science, offering rigorous control over thermodynamic variables alongside atomistic spatial and temporal resolution. In DFT, the electronic structure is obtained by solving the Kohn-Sham self-consistent field (SCF) equations and diagonalizing the Hamiltonian matrix to extract its eigenvalues. By contrast, both geometry optimization and MD rely on potentials: geometry optimization locates minima to identify stable atomic configurations, whereas MD integrates Newton’s equations of motion to simulate the real-time evolution of atomic positions and velocities. Despite their widespread use, these techniques face inherent limitations. The cost of DFT scales as O(N3) (or worse) with the number of atoms N due chiefly to Hamiltonian diagonalization, thereby constraining studies to relatively small quantum systems[1]. Conversely, classical MD, though orders of magnitude faster, depends on empirical interatomic potentials (IAPs) [or force fields (FFs)] that often lack the transferability and accuracy required for complex chemistries.
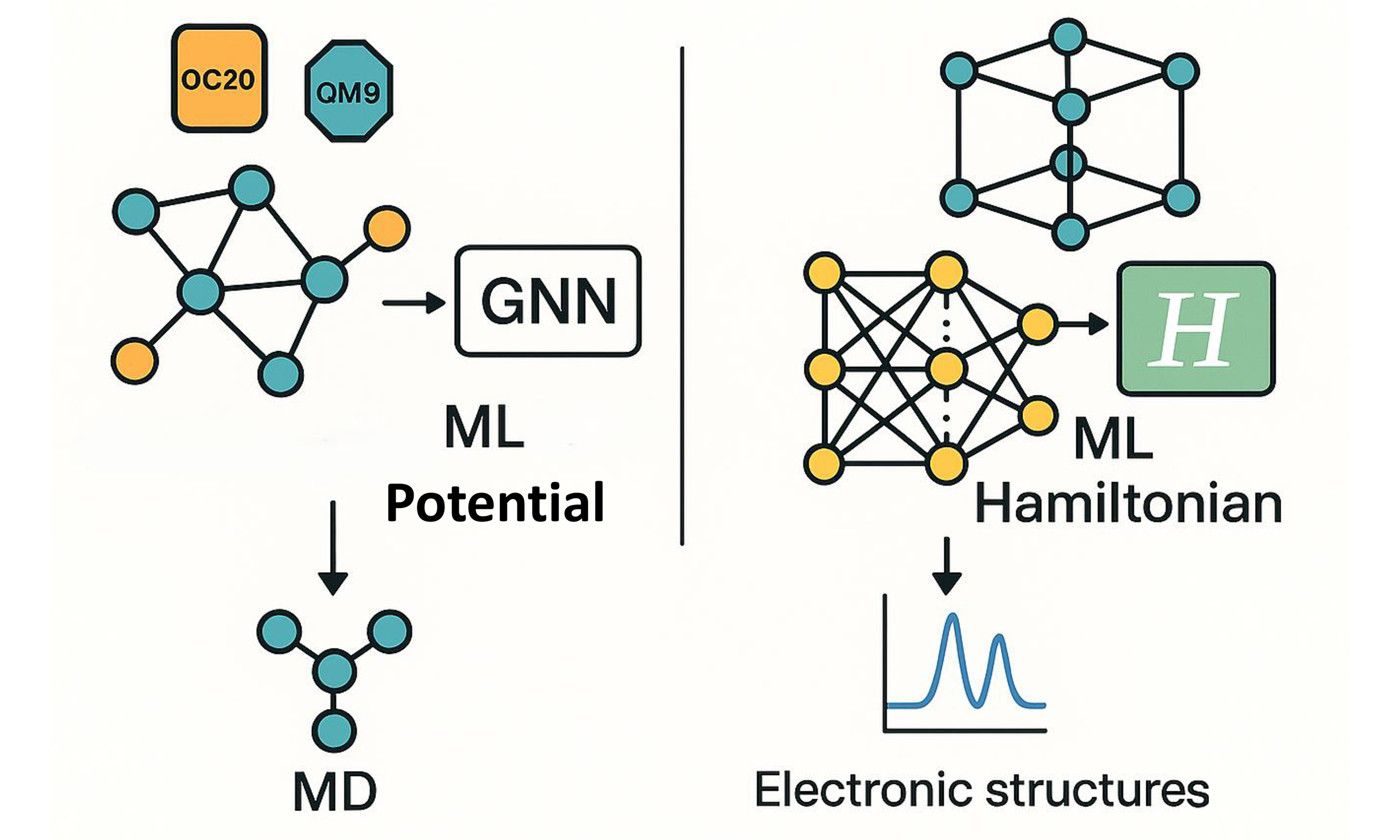
Bridging the gap between accuracy and scalability has emerged as a central challenge. Machine learning (ML) offers a transformative pathway by leveraging high-fidelity ab initio data to construct surrogate models that operate efficiently at extended scales. ML interatomic potentials (ML-IAPs), or ML force fields (ML-FFs), implicitly encode electronic effects through training on quantum reference datasets, enabling faithful recreation of the potential energy surface (PES) across diverse chemical environments without explicitly propagating electronic degrees of freedom. Their robustness hinges on accurately learning the mapping from atomic coordinates to energies and forces. In parallel, ML Hamiltonian (ML-Ham) approaches seek to predict electronic potentials using methods such as ML-derived Kohn–Sham potentials[2], deep Hamiltonian neural networks (DHNNs)[3], Hamiltonian graph neural networks (GNNs)[4] and deep tight-binding models[5]. Different from conventional ML approaches (structure-property), ML-Ham methods (structure-physics-property) provide clearer physical pictures and explainability, delivering near-ab initio accuracy for quantities ranging from band structures and Berry phases to electron–phonon couplings.
In this Review, we survey recent algorithmic and architectural advances in ML-driven IAPs and Hamiltonian models, with particular emphasis on symmetry-aware GNNs, data-efficient training strategies and interpretability techniques and their successful applications. Moreover, we highlight the critical challenges in this field, including data fidelity, model generalizability and computational scalability. Finally, we also outline promising future directions poised to extend ML-accelerated simulations from small molecules to complex, multiscale materials systems.
ML-IAPS
ML-IAPs or MLFFs have emerged as a transformative approach in computational materials science, offering a data-driven alternative to traditional empirical FFs[6,7]. By leveraging deep neural network architectures, ML-IAPs directly learn the PES from extensive, high quality quantum mechanical datasets[8], thereby obviating the need for fixed functional forms, such as conventional Lennard-Jones or bond-order potentials, and instead optimizing large parameter spaces via automatic differentiation[7].
The principal advantage of ML-IAPs lies in their capacity to reproduce atomic interactions, including energies, forces and dynamical trajectories, with high fidelity across chemically diverse systems[8]. When trained on ab initio molecular dynamics (AIMD) trajectories, these models facilitate accurate simulations over extended temporal and spatial scales[9], achieving superior accuracy relative to conventional potentials while maintaining the computational efficiency required for large-scale materials modeling[10].
Material representation
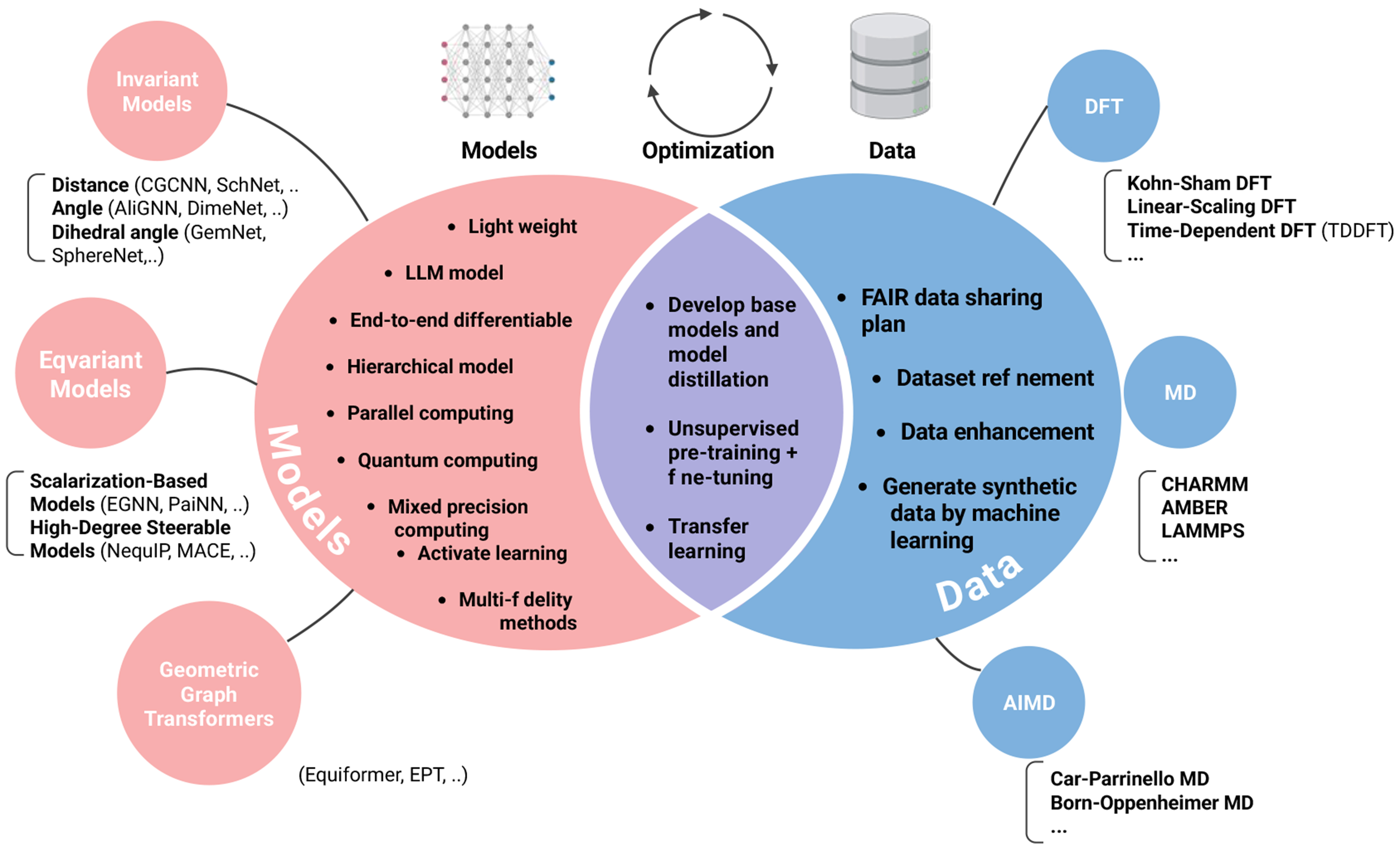
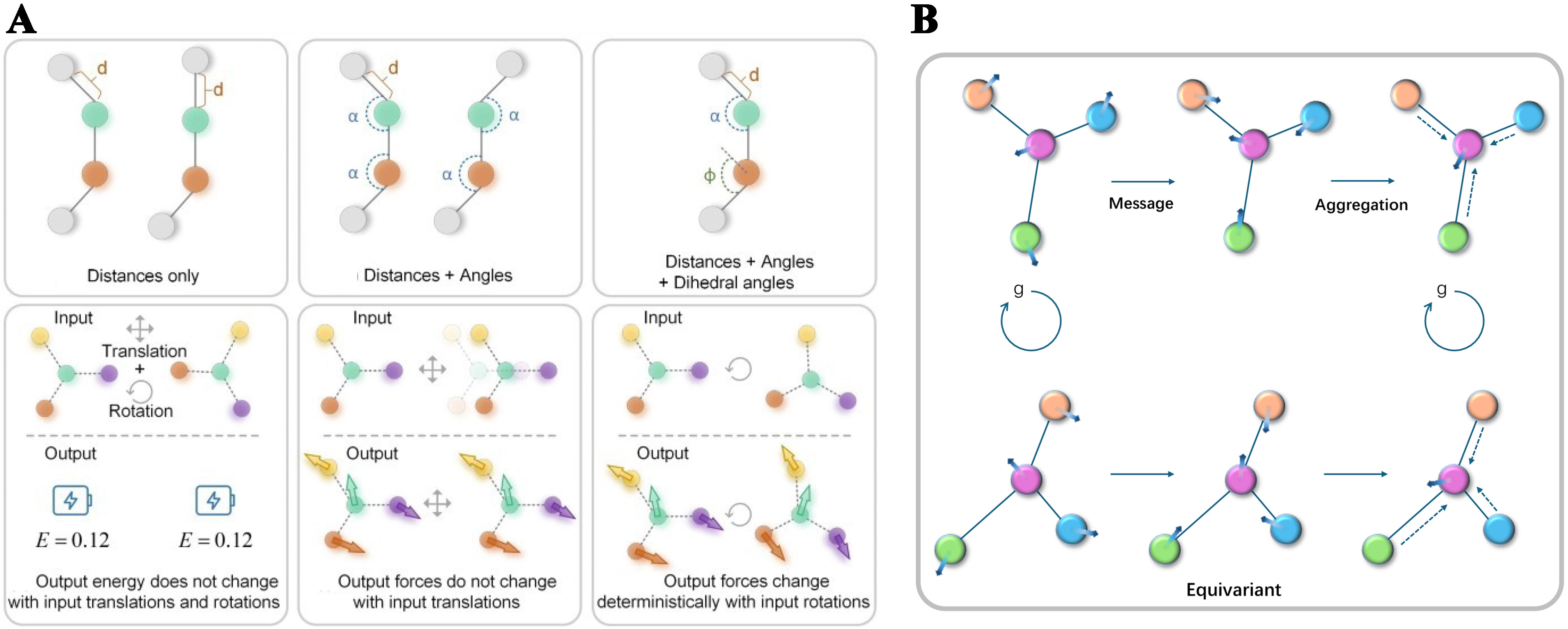
Early ML-IAPs relied on handcrafted invariant descriptors to encode the potential-energy surface by using bond lengths and subsequently bond angles and dihedral angles [Figures 1 and 2A]. The advent of GNNs has transformed this landscape by enabling end-to-end learning of atomic environments. In particular, equivariant architectures preserve rotational and translational symmetries, while large language models (LLMs) such as ChemBERTa[12] and MolBERT[13] have been repurposed to generate chemically informed embeddings. Together, these advances have driven the development of a suite of state-of-the-art (SOTA) ML-IAP frameworks that combine symmetry-aware message passing with data-driven feature representations[10] [Figure 1].
Figure 1. An overview of deep IAP development and outlook on associated data, models, and optimization strategies. IAP: Learning interatomic potential.
Figure 2. (A) Structural representations: integrating structural features into GNNs, including distance only, both distance and angles, and all distance, angles, and dihedral angles. The concepts of different structural representations within the context of energy (scalar) and force (vector) prediction[11]. The d, α, and Φ represent the bond length, bond angle, and dihedral angle, respectively; (B) Schematic diagram of massage passing and aggregation in equivariant representations of crystalline structures under a rotation operation. GNNs: Graph neural networks.
Embedding physical symmetries directly into network architectures, rather than applying symmetry constraints only to final invariant outputs, has been instrumental in advancing ML-IAPs. Equivariant layers maintain internal feature representations that transform under rotations and translations according to the underlying symmetry group, guaranteeing that scalar predictions (for example, total energy) remain invariant while vector and tensor targets (such as forces and dipole moments) exhibit the correct equivariant behavior[14] [Figure 2]. By unifying invariant and equivariant features throughout the model, these architectures achieve both greater data efficiency and improved accuracy across downstream tasks, as exemplified by NequIP exploration of higher-order tensor contributions to performance[14]. Furthermore, this approach parallels classical multipole theory in physics, encoding atomic properties as monopole, dipole and quadrupole tensors and modeling their interactions via tensor products, integrating long-standing theoretical formalisms into a modern deep-learning framework[15].
Equivariant models (also named geometrically equivariant models) explicitly embed the inherent symmetries of physical systems, which is critical for accurately modeling tensorial quantities such as spin Hall conductivity and piezoelectric coefficients[16]. Many materials problems exhibit three-dimensional translation, rotation and/or reflection invariances, corresponding respectively to the Euclidean groups SO(3) (rotations), SE(3) (rotations and translations) and E(3) (including reflections). Unlike approaches that rely on data augmentation to approximate symmetry, equivariant architectures integrate these group actions directly into their internal feature transformations, ensuring that each layer preserves physical consistency under the relevant symmetry operations. However, enforcing strict equivariance throughout the network is not universally necessary: judicious relaxations of equivariance constraints have been shown to enhance model generalization and computational efficiency in certain applications[17].
Furthermore, as the scale and complexity of materials datasets continue to grow, the computational burden of fully E(3)-equivariant models increases steeply. An emerging strategy is to construct “lightweight” architectures that disentangle rotational and translational symmetries by employing only SO(3)-equivariant operations alongside translation-invariant scalar and vector features[18]. By partitioning high-order tensor products into rotationally equivariant and purely invariant components, these models markedly reduce the cost of tensor contractions without sacrificing the symmetry-preserving properties essential for accurate ML-IAP development[11].
Beyond atomic force vectors, spin degrees of freedom likewise transform as vectors under three-dimensional Euclidean symmetries, motivating the extension of ML-IAPs to magnetic materials. MagNet[19] learns magnetic force vectors by mapping combined atomic and spin configurations to forces computed via DFT, embedding E(3)-equivariance within its network layers to ensure physically consistent transformations. In parallel, SpinGNN[20] introduces two specialized architectures [the Heisenberg edge graph neural network (HEGNN) and the spin distance edge graph neural network (SEGNN)] to represent Heisenberg exchange and spin-lattice couplings through equivariant message passing, thereby capturing multi-body and higher-order spin interactions with high fidelity.
Deep potential molecular dynamics (DeePMD)[21] formulates the total potential energy as a sum of atomic contributions, each represented by a fully nonlinear function of local - environment descriptors defined within a prescribed cutoff radius. The DeePMD framework, implemented in DeePMD-kit, has been trained on extensive DFT datasets of the order of 106 water configurations, achieving energy mean absolute errors (MAEs) below 1 meV per atom and force MAE under 20 meV/Å. By encoding smooth neighboring density functions to characterize atomic surroundings and mapping these descriptors through deep neural networks, Deep Potentials attain quantum mechanical accuracy with computational efficiency comparable to classical MD, thereby enabling atomistic simulations at spatiotemporal scales hitherto inaccessible.
Data representation: balance between quality and quantity
Notwithstanding these advancements, the predictive accuracy of even SOTA ML models remains fundamentally limited by the breadth and fidelity of available training data. Publicly accessible experimental materials datasets are orders of magnitude smaller than those in image or language domains, impeding the construction of universally transferable and highly precise potentials. DFT datasets with meta-generalized gradient approximation (meta-GGA) exchange-correlation functionals offer markedly improved generalizability compared to semi-local approximations[22], and thus provide a solid foundation for training universal models[23] [Table 1].
Overview of common benchmark datasets for ML-IAPs
| Dataset | Description | Data scale | Benchmark tasks | URL |
| QM9[24] | Stable small organic molecules (C, H, O, N, F; ≤ 9 heavy atoms) | 134 k molecules (~1 × 106 atoms) | Molecular property prediction (energies, HOMO/LUMO, dipoles) | https://figshare.com/collections/Quantum_chemistry_structures_and_properties_of_134_kilo_molecules/978904 |
| MD17[25] | MD trajectories for 8 small organic molecules (e.g., benzene, ethanol) | ~3-4 M configurations (~1 × 108 atoms) | Energy and force prediction | http://quantum-machine.org/datasets/#md-datasets |
| MD22[26] | Large molecules/biomolecular fragments (42-370 atoms) | 0.2 M configurations (~1 × 107 atoms) | Energy and force prediction for large systems | https://www.openqdc.io/datasets/md22 |
| ANI-1[27] | Small organic molecules [C, H, N, O; (CNO) ≤ 8 atoms] | 20 M DFT conformations (~5 × 106 atoms) | Molecular potential training; energy prediction | https://figshare.com/collections/_/3846712 |
| ANI-1x[28] | Small organic molecules (C, H, N, O) | 5 M DFT conformations (~5 × 106 atoms) | Molecular potential training; energy prediction | DOI: 10.6084/m9.figshare.c.4712477.v1 |
| ANI-1ccx[29] | Subset of ANI-1x recalculated at CCSD(T)/CBS level | 0.5 M high-accuracy conformations (~5 × 105 atoms) | High-precision energy prediction | DOI: 10.6084/m9.figshare.c.4712477.v1 |
| ANI-2x[30] | Organic molecules including S, F, Cl (H, C, N, O, S, F, Cl) | 9,651,712 conformers (~9.7 × 106 atoms) | Energy and force prediction across extended chemistry | https://zenodo.org/records/10108942 |
| ISO17[31] | C7H10O2 isomer dynamics | 0.645 M configurations (~1 × 107 atoms) | Energy/force generalization over chemical and conformational changes | DOI: 10.1038/sdata.2018.75 |
| SPICE[32] | Bio-relevant molecules and complexes (15 elements) | 1.1 M conformers (~1 × 108 atoms) | Energy/force prediction for biomolecular interactions | DOI: 10.5281/zenodo.7338495 |
| OC20[33] | Adsorbate-surface combinations on transition-metal facets | 1.28 M DFT relaxations (~2.65 × 108 single-point evaluations) | Adsorption energy, reaction pathway, structure optimization | https://fair-chem.github.io/catalysts/datasets/oc20.html |
| OC22[34] | Oxide electrocatalyst surfaces and adsorbates | 62,331 DFT relaxations (~9.85 M single-point calculations) | S2EF, IS2RE, IS2RS for oxide catalysts | https://fair-chem.github.io/catalysts/datasets/oc22.html |
| Materials Project[35] | Bulk inorganic crystals (all element combinations) | 130 k optimized crystal structures | Formation energy, band gap, elastic moduli | https://materialsproject.org/ |
| Matbench[36] | 13 derived property tasks from Materials Project | 312-132 k samples per task (~3 × 105 total) | Multi-property materials predictions (energy, gap, moduli) | https://github.com/hackingmaterials/matbench |
However, the majority of current repositories remain at Perdew–Burke–Ernzerhof (PBE) level accuracy[37], highlighting the need to incorporate more sophisticated electronic treatments (for example, Hubbard U corrections or meta-GGA/hybrid functionals) to capture complex many-body interactions. Recent work exemplifies this strategy: the high-fidelity data–based M3GNN framework leverages meta-GGA datasets alongside an SE(3)-equivariant GNN to resolve subtle structural and electronic features, establishing a new benchmark for materials-property prediction accuracy[38] [Figure 1].
Model efficiency is equally critical for scaling ML-IAPs to large-system simulations. A linearized NequIP architecture[39] reduces the complexity of tensor contractions while preserving core equivariant operations, yielding substantial decreases in inference cost with no measurable loss in force-prediction accuracy. This demonstration confirms that judicious architectural simplifications can reconcile high fidelity with practical throughput. In a complementary advance, the Meta ML-IAP framework[40] couples comprehensive data curation pipelines with a modular network design to enhance both generalizability and computational performance. By leveraging curated high-fidelity datasets alongside streamlined equivariant layers, this approach extends ML-driven potentials to multicomponent and structurally intricate materials systems without sacrificing efficiency.
Although MD simulations yield atomistic trajectories, the resulting datasets remain constrained by both label noise and limited sampling[41]. Classical or semi-empirical potentials introduce systematic errors in energy and force labels, while the high cost of MD restricts simulations to nanosecond-microsecond timescales and nanometre-micrometre lengthscales, impeding the observation of rare events and long-range phase transitions. Furthermore, trajectories typically originate from a single initial configuration, yielding uneven phase-space coverage and restricted structural diversity[42]. To overcome these challenges, data quality may be enhanced by adopting higher-fidelity potential models or experimental calibration, and dataset size expanded via enhanced sampling techniques, multiscale simulations or integration with experimental measurements, thereby producing ML-IAPs that are both robust and generalized.
Effective data-sharing initiatives are critical for accelerating materials discovery and model development. The findable, accessible, interoperable and reusable (FAIR) framework[43], and platforms such as the Materials Data Facility[44], the Materials Project, OQMD, NOMAD and 2DMatPedia now host extensive collections of crystal structures, simulation outputs and derived properties. Leveraging these repositories enables the assembly of diversified, high-quality training sets, streamlines data curation and facilitates benchmarking against standardized datasets. Active learning monitoring model uncertainty and selectively incorporating high-uncertainty samples into the training set has proven effective in exploring chemical space more efficiently, reducing labeling effort and improving generalizability in materials modeling[45,46]. Likewise, pretraining on lower-fidelity structural databases offers a promising route to broaden coverage with manageable computational costs[47].
Defining the chemical and structural breadth of a training dataset establishes its “target space”, and different coverage regimes give rise to distinct modeling strategies ranging from general purpose zero shot frameworks to fine-tuned and bespoke potentials. General purpose approaches, however, face two intrinsic limitations. First, existing materials databases do not uniformly sample the periodic table, resulting in pronounced element wise imbalances and variable data quality. Second, these models often struggle to represent or relax complex architectures such as reconstructed surfaces, defect networks or low symmetry phases with the fidelity required for quantitative predictions. For example, although total energy estimates for surface geometries may achieve moderate accuracy, they frequently fail to resolve surface specific energetics (for instance, cleavage or adsorption energies), underscoring a shortfall in generalization across disparate datasets and property domains[48].
One avenue to redress dataset imbalance is data augmentation, in which underrepresented regions of chemical and structural space are populated by additional configurations generated through high-throughput simulations[49]. Concurrently, tailored IAPs designed for structurally complex materials have demonstrated markedly improved performance. For example, DefiNet augments the host graph with vacancy markers and employs defect-aware message passing to capture interactions between vacancies, substitutions and pristine atoms, while fine-tuned MLFFs for defected crystals revise local‐environment descriptors and network capacity to accommodate disrupted periodicity[50]. Through systematic refinement of descriptor schemes or the integration of higher-capacity, symmetry-preserving architectures, these bespoke models extend the applicability of ML-IAPs to materials with intricate defect landscapes.
ML-IAPs models: balance between complexity and efficiency
Although advanced network architectures and sophisticated optimization schemes have propelled ML-IAPs to unprecedented accuracy, they also introduce notable challenges. As models become more complex, they may overfit the training data, while simpler models may lose important details[51]. Iterative optimization routines further complicate matters by permitting error accumulation across successive parameter updates, which can undermine predictive consistency. A compelling strategy to mitigate these issues may be the development of fully differentiable, high-precision end-to-end frameworks, in which the final loss can be backpropagated through every component of the modeling pipeline, ensuring uniform gradient flow and reducing the potential for both overfitting and numerical drift. Fully differentiable architectures have become foundational to modern GNN‐based IAPs, replacing fixed structural descriptors with highly parameterized functions that are optimized end-to-end via stochastic gradient descent. By enabling gradient signals to propagate through every model component, this paradigm avoids arbitrary handcrafted features and ensures that learned representations adapt dynamically to diverse atomic environments. The DeepMind Allegro framework exemplifies this strategy, leveraging fully differentiable message‐passing layers and learned radial functions to accelerate convergence and enhance both energy and force accuracy[52]. End-to-end differentiability thus underpins improved training efficiency, model adaptability and generalizability across complex materials systems.
A recent paradigm, termed effective MD, offers a compelling route to reconcile the trade‐off between fidelity and throughput in atomistic simulations[53]. In this framework, high‐accuracy AIMD data are used to parameterize streamlined force‐evaluation kernels via tailored optimization routines. By distilling complex force‐field representations into efficient surrogate models, effective MD delivers robust dynamical trajectories with significantly lower computational cost than full AIMD, while keeping predictive accuracy. This approach thus exemplifies how judicious integration of high‐fidelity training data and optimized model architectures can extend the reach of IAPs to time‐ and length‐scales previously accessible only to classical MD.
In all cases, a careful balance between computational expense and predictive accuracy is essential. SOTA equivariant and multi-fidelity GNN IAPs have pushed the limits of energy and force prediction accuracy across a breadth of materials and molecular systems. NequIP demonstrates exceptional data efficiency, achieving sub-meV energy errors and force errors on the order of tens of meV/Å in a complex reactive environment[14]. CHGNet, pretrained on over 1.5 M DFT trajectories, reaches energy MAEs below 30 meV/atom with force errors under 70 meV/Å for inorganic crystals[54]. SevenNet-MF leverages multi-fidelity training to deliver energy MAEs of ~10.8 meV/atom and force MAEs of ~18.3 meV/Å[38]. EquiformerV2 is an improved equivariant transformer, which achieves energy MAEs down to 9.6 meV/atom with force MAEs near 43 meV/Å when pretrained on OMat24 datasets, and maintains competitive errors (~20 meV/atom) under Matbench-Discovery compliance[55]. Equivariant smooth energy network (eSEN) attains leading static test-set performance on molecular benchmarks, with energy MAEs around 0.13 eV/atom and force MAEs as low as 1.24 eV/Å[40], and achieves energy MAEs down to 18 meV/atom under Matbench-Discovery compliance[55] which is considered to be the best performing model currently. These results underscore the potential of advanced equivariant models to deliver near-chemical accuracy while balancing computational costs [Figure 3]. Although these models are expected to achieve precision below 1 meV/atom on given datasets, most of them have a huge number of parameters. For example, the recent GNoME model[57] has 16.2 million parameters. The recent proprietary MatterSim model, trained on a 17-million-structure dataset, can reach up to 182 million parameters[48]. The high computational demand of quantum mechanics calculations has traditionally limited their application in ML-IAPs. Thus, advanced training architectures should be considered in this domain to accelerate model training and prediction.
Figure 3. Architectures of SOTA ML-IAP models. (A) NequIP, a data-efficient E(3)-equivariant GNN[14]; (B) CHGNet, a crystal Hamiltonian GNN[54]; (C) eSEN, a smooth, expressive ML-IAP[40]; (D) SevenNet-MF, a multi-fidelity equivariant GNN[38]; (E) EquiformerV2, an improved equivariant transformer[56]. SOTA: State-of-the-art; ML-IAP: machine learning interatomic potential; GNN: graph neural network; eSEN: equivariant smooth energy network.
Model and hardware optimization
Hierarchical model architectures may address multiscale complexity by cascading predictors of increasing fidelity. For example, one can use initial modules with low-cost and coarse-grained networks to generate rough potentials, whereas subsequent stages apply high-resolution models to refine these predictions. This tiered strategy can markedly reduce computational costs without compromising accuracy[27]. In addition, mixed-precision computing smartly mixes single- and double-precision calculations during training, helping to reduce computation time and cost while still keeping the results accurate and stable. Finally, parallelization schemes through data-parallel or model-parallel across multicore CPUs and GPUs can enable near-linear throughput scaling, extending ML-driven simulations to larger and more structurally complex materials systems. Additionally, parallel computing techniques can significantly enhance computational efficiency. Utilizing high-performance computing clusters or GPU acceleration can process multiple tasks simultaneously, reducing overall computation time. Especially in training large models, parallel computing can significantly reduce training time. Furthermore, developing models suitable for quantum computers may break this limitation, though it remains controversial whether quantum bits or quantum computing can practically accelerate quantum chemistry calculations[58,59].
Additionally, transfer learning and multi-fidelity frameworks offer a potent means to alleviate the dependence on large, high-fidelity datasets [Figure 1]. Transfer learning accelerates adaptation to new chemical spaces by reusing representations learned from related tasks[45,49]. In practical terms, molecular potentials pretrained on datasets such as ANI-1 can be fine-tuned for materials systems, thereby reducing the volume of costly DFT annotations required[27]. Multi-fidelity approaches further decrease computational expense by integrating low-precision and high-precision data within a unified training hierarchy. More recently, AI-predicted structures have been employed as initial configurations for subsequent DFT relaxations, providing an efficient compromise between speed and accuracy. Finally, advanced robustness techniques, such as domain adaptation and meta-learning[60], are increasingly being incorporated into equivariant GNN architectures to bolster generalizability across diverse materials domains.
ML HAMILTONIAN
Although ML-driven IAPs have transformed atomic-scale simulations, an equally compelling frontier is the creation of machine-learning Hamiltonian, ML-Ham, for direct electronic-structure prediction [Figure 4A]. These “electronic-scale” networks aim to eliminate the costly SCF loops inherent to conventional Kohn-Sham DFT, in which repeated updates of the electron density and Hamiltonian scale cubically with system size. DHNNs, trained on libraries of precomputed DFT Hamiltonian matrices, instead learn a direct mapping from atomic coordinates to the Hamiltonian operator, thereby bypassing iterative SCF convergence and delivering near–first-principles accuracy at a fraction of the computational expense.
Figure 4. (A) Summary of ML-Ham architectures, models, and physical properties; (B) Examples of ML-Ham applications, including band gaps, charge densities[61], noncolinear magnetism, excited-state dynamics[62], EPC[63], quantum transport[64], spin-orbit coupling[65] and amorphous materials[66]. ML-Ham: Machine learning Hamiltonian; EPC: electron-phonon coupling.
However, the Hamiltonian is intrinsically a high-order tensor whose elements transform nontrivially under rotations, translations and spatial inversions, imposing strict equivariance requirements on any predictive model [Figure 5A]. Early neural approaches such as SchNorb[68] demonstrated that one could learn approximate Hamiltonians, but they achieved equivariance only indirectly by augmenting training data with random rotations, rather than embedding symmetry in the model itself. The true breakthrough arrived with E(3)-equivariant neural networks, which incorporate group-theoretical symmetry operations directly into their layers [Figure 5B]. PhiSNet[69], for example, enforces exact E(3) equivariance by construction, ensuring that its predicted Hamiltonian matrices transform correctly under all rigid motions and thereby delivering greater accuracy and transferability.
Figure 5. Equivariant DHNNs. (A) The fundamental physics of DHNNs is to predict the Hamiltonian rather than directly predicting electronic properties from structures. Equivariance ensures that symmetries, such as rotation, translation, and inversion, are explicitly preserved in Hamiltonian predictions; (B) Equivariance of the Hamiltonian under spatial rotations and spin-orbit coupling. Schematic wavefunctions and Hamiltonian matrices are shown for systems without SOC (structures a1 and a2, related by a 90° rotation) and with SOC (structures b1 and b2). In the non-SOC case, the hopping parameters transform into one another by a unitary rotation, illustrating the requirement that the Hamiltonian remains equivariant under spatial rotations. When SOC is included, spin and orbital degrees of freedom become entangled and must jointly transform under the same global rotations, as demonstrated by the corresponding rotated configurations[67]. DHNNs: Deep Hamiltonian neural networks.
Despite achieving impressive accuracy, the early E(3) DHNNs faced significant computational bottlenecks. This was because they directly encoded E(3) or SE(3) symmetries through the tensor field network (TFN) approach[70]. The tensor product operations in this approach rely on Clebsch-Gordan coefficients, resulting in O(L6) computational complexity. This limitation severely restricted their practical application to systems with higher tensor orders or larger atomic numbers. Recent architectural innovations have addressed these efficiency challenges primarily through tensor product optimization. A key insight from the equivariant spherical channel network[71] demonstrated that aligning the primary axis with interatomic bond directions dramatically simplifies calculations by reformulating SO(3) convolutions as SO(2) operations, reducing complexity to O(L3). This SO(2) approach has become central to several SOTA models, e.g., the architecture design of DeepH-2[72], SLEM[73] and WANet[74] [Figures 4 and 5A].
Beyond architectural innovations, accuracy improvements have also come from better loss function design. WANet introduces the physically-motivated Wavefunction Alignment Loss (WALoss), which surpasses simple element-wise error metrics by directly enforcing alignment between predicted and ground-truth wavefunctions. Additionally, TraceGrad[75], a lightweight plug-in module, enhances accuracy using SO(3)-invariant trace quantities as supervisory signals which have been integrated with QHNet[76] and DeepH-E3[67] [Figure 6A]. This approach guides the development of high-quality equivariant representations, achieving good prediction performance.
Figure 6. Architectures of SOTA DHNN models. (A) DeepH-E3, An E(3)-equivariant neural network representation of DFT Hamiltonian[67]; (B) HamGNN, a data-driven E(3) equivariant GNN for the electronic Hamiltonian matrix[77]; (C) DeePTB-E3, a novel deep learning model for predicting multiple quantum operators[73]. SOTA: State-of-the-art; DHNN: deep Hamiltonian neural network; DFT: density functional theory; GNN: graph neural network.
Looking ahead, the evolution of DHNNs will hinge on three interlinked challenges. First, achieving true universality and scalability demands that DHNNs generalize across the full periodic table and extend to very larger systems. This is a goal that will require innovations in strictly local message passing, hierarchical graph decompositions and delta-learning schemes to drive computational cost toward linear scaling. Second, broadening the applicability of these architectures to encompass richer physical phenomena from spin-orbit coupling and non-collinear magnetism to excited state dynamics and quantum transport [Figure 4B]. This will call for modular and multi-task frameworks capable of integrating additional Hamiltonian terms and perturbative operators without sacrificing symmetry rigor. Finally, unlocking the full scientific potential of DHNNs rests on enhancing interpretability and trust, which is essential for mechanistic insight, model validation and widespread adoption. It needs embedding physics-informed constraints, developing graph-based explainability tools and rigorous uncertainty quantification [Table 2].
Summary of DHNNs, including model name, model type, code repository, data source and link, and a brief description of their usage
| Model | Type | Code repository | Data source | Usage | Data link |
| DeepH[4] | Message-passing DFT Hamiltonian network; dense invariant GNN | https://github.com/mzjb/DeepH-pack | Zenodo | Uses DFT Hamiltonian matrices & energies generated on Materials Project (via ABACUS, OpenMX, FHI-aims, SIESTA) to train a direct mapping from crystal structure to Hamiltonian | https://zenodo.org/records/6555484 |
| DeepH-E3[67] | E(3)-equivariant attention transformer | https://github.com/Xiaoxun-Gong/DeepH-E3 | Provided with paper | Uses Materials Project DFT structures & energies released alongside the publication to train an equivariant attention/Transformer architecture - achieving strict rotational & translational equivariance | https://www.nature.com/articles/s41467-023-38468-8 |
| HamGNN[77] | E(3)-equivariant convolutional GNN for tight-binding Hamiltonian | https://github.com/QuantumLab-ZY/HamGNN | Zenodo (pretrained models and datasets) | Trained on DFT-generated tight-binding Hamiltonian matrices for QM9 molecules, carbon & silicon allotropes, SiO2 polymorphs, and BixSeγ compounds - enabling high-accuracy transfer to large-scale systems (e.g., Moiré bilayer MoS2, Si dislocation supercells) | Pretrained models: DOI: 10.5281/zenodo.8147631 Training data: DOI: 10.5281/zenodo.8157128 |
| DeepH-hybrid[78] | Hybrid-functional DFT Hamiltonian predictor | https://github.com/aaaashanghai/DeepH-hybrid | Zenodo | Uses hybrid-functional Hamiltonian & frequency-response (χxx) data covering various twist angles of Moiré bilayer MoS2; bypasses SCF iterations to directly predict hybrid-functional Hamiltonians | https://zenodo.org/records/13444159 |
| DeepH-DFPT[79] | DFPT-enhanced Hamiltonian network | interface code + datasets on Zenodo | Zenodo | Includes FHI-aims computed DFPT phonon spectra & force-constant data to introduce phononic corrections into Hamiltonian predictions - improving accuracy for phonon-response properties | https://zenodo.org/records/13943187 |
| HarmoSE[80] | Two-stage SO(3)-equivariance + expressiveness framework | N/A | Materials Project | Stage 1: group-theory neural layers extract SO(3)-equivariant baseline Hamiltonians; stage 2: non-linear 3D graph Transformer refines them for high accuracy | N/A |
| xDeepH[81] | E(3)×{I,T}-equivariant spin-orbital GNN | https://github.com/mzjb/xDeepH | Zenodo | Uses constrained-DFT (OpenMX/DeepH-pack) Hamiltonian & overlap matrices for magnetic superstructures (e.g., CrI3, skyrmion lattices) to train a mapping from structure + spin to Hamiltonian | https://zenodo.org/records/7669862 |
| DeepH-PW[82] | Real-space reconstruction of plane-wave DFT → atomic-orbital Hamiltonian | https://github.com/Xiaoxun-Gong/HPRO | Zenodo | Provides reconstructed AO Hamiltonian datasets converted from PW DFT outputs for 300 bilayer-graphene and 256 MoS2 supercells - used to train the real-space reconstruction network | DOI: 10.5281/zenodo.13377497 |
| WANet[74] | Scalable Hamiltonian prediction via SO(2) convolutions, Mixture-of-Experts & MACE density trick | N/A | PubChemQH dataset | Builds on eSCN convolutions (reducing complexity), sparse experts for different length scales, and many-body density trick to predict full Hamiltonian matrices for very large molecules | N/A |
| DeepH-UMM[83] | Universal Materials Model for Hamiltonian | N/A | N/A | Built on > 10,000 Materials Project DFT Hamiltonian matrices spanning 89 elements to create a universal model transferable across element combinations and crystal structures | N/A |
| MEHnet[84] | Multi-task CCSD(T)-trained molecular Hamiltonian + properties predictor | https://github.com/htang113/Multi-task-electronic | FigShare | Includes scripts to build the CCSD(T) training dataset, train the multi-task network on energies, dipoles, orbitals, etc., and apply it to both small hydrocarbons and QM9 benchmarks | DOI: 10.6084/m9.figshare.25762212 |
| HamGNN-EPC[85] | Electron–phonon coupling workflow leveraging HamGNN | https://github.com/QuantumLab-ZY/HamEPC | N/A | Uses HamGNN-predicted Hamiltonian matrices & gradients together with Phonopy/DFPT data to accelerate computation of electron–phonon coupling matrices, carrier mobilities, superconducting transition temperatures, etc. | N/A |
| U-HamGNN[61] | Unsupervised pretrained E(3)-equivariant HamGNN | https://github.com/QuantumLab-ZY/HamGNN | Zenodo | Conducts unsupervised pretraining on a large unlabeled crystal-structure database to learn E(3)-equivariant representations, then fine-tunes on small labeled DFT Hamiltonian sets to boost initialization and generalization | https://zenodo.org/records/10827117 |
| HamGNN-Q[86] | E(3)-equivariant GNN for charged-defect tight-binding Hamiltonian | N/A | OpenMX | Trained on TB Hamiltonian matrices for GaAs charged defects (vacancies, interstitials, substitutions at Q = 0, ±3) to learn structure + background-charge → Hamiltonian mapping with reciprocal-space band-energy regularization | N/A |
| SchNOrb[67] | SchNet-based molecular orbital & wavefunction predictor | https://github.com/atomistic-machine-learning/SchNOrb | Quantum-machine.org | Uses QM9 dataset [134 k small molecules at B3LYP/6-31G(2df,p)] to predict molecular orbital coefficients and electron densities | http://www.quantum-machine.org/datasets/ |
| DeepTB[87] | Deep-learning Slater–Koster tight-binding Hamiltonian; supports SOC | https://github.com/deepmodeling/DeePTB | DeePTB examples | Provides Slater–Koster TB parameters for graphene, MoS2 and bulk phases (VASP/Wannier90) to train deep TB models for large-scale, near-DFT-level simulations | https://github.com/deepmodeling/DeePTB/tree/main/examples |
Deep Hamiltonian model: generality and scalability
DHNNs have rapidly emerged as a transformative approach for surmounting the steep computational demands of conventional quantum-mechanical methods such as Kohn-Sham DFT [Table 2]. Yet despite their promising accuracy and efficiency, DHNNs remain in an infant stage. Their evolution into a truly universal tool for materials science and quantum chemistry depends on overcoming two intertwined challenges. One is the generality that the capacity to learn Hamiltonians across the full breadth of chemical space and structural complexity. The other is the scalability, which is the ability to maintain accuracy and computational efficiency as system size grows. Addressing these twin imperatives is essential to unlock DHNN potential as a high-throughput, first-principles surrogate for large-scale quantum simulations.
Despite significant progress by architectures such as DeepH and HamGNN toward broader material coverage, existing DHNNs still struggle with true generality [Figure 6A and B]. To date, these models have been developed and validated almost exclusively on well-ordered crystalline systems, leaving out inherently disordered amorphous networks[88], defected materials[89] and high-entropy alloys[90], that pervade real-world materials. Disordered systems, for example, are ubiquitous in technologically relevant materials. However, these systems lack the long-range translational symmetry characteristic of well-ordered crystals, and they typically exhibit high configurational entropy. This combination results in a vast and highly diverse landscape of local atomic environments, where each atomic neighborhood can be distinct. The current message-passing schemes predominantly employed by DHNNs inherently operate with limited receptive fields. These schemes are designed to learn relationships by primarily considering local atomic structures when mapping to Hamiltonian matrix elements. Consequently, such models struggle to effectively capture the nuances of structural disorder that extend beyond these local regions. Such structural disorder poses a formidable challenge: without mechanisms to capture the irregular local environments and stochastic atomic arrangements characteristic of these systems, DHNNs risk losing both robustness and transferability. Closing this gap by integrating disorder aware descriptors, adaptive message passing schemes and targeted data augmentation will be essential for DHNNs to become universally reliable electronic structure surrogates.
Scalability poses a fundamental bottleneck for DHNNs. As the number of atoms grows, both the dimensionality of the Hamiltonian matrix and the complexity of interatomic couplings increase combinatorially. The strictly localized equivariant message-passing (SLEM) framework[73] [Figure 6C] overcomes this by enforcing a hard cutoff on each node’s receptive field, so that messages propagate only within a fixed local neighborhood. By confining interactions in this way, SLEM reduces the overall computational cost to scale linearly with system size, while its inherently local structure lends itself to straightforward parallelization. Thereby, it enables accurate Hamiltonian predictions for truly large and complex materials.
Regarding the gold-standard accuracy, two complementary strategies have emerged in DHNNs: delta learning and multi-task training. In the delta learning paradigm exemplified by the DeepKS framework[91], the network is trained to predict only the difference between a low-cost GGA (PBE) Hamiltonian and the corresponding high-accuracy hybrid (HSE06) result, thereby attaining hybrid-functional precision at a computational cost comparable to PBE[92]. In contrast, the multi-task electronic Hamiltonian network (MEHnet)[84] learns to map atomic geometries simultaneously to Kohn-Sham Hamiltonians across multiple levels of theory and basis sets, endowing the model with robust transferability. Although initially trained on small molecules, MEHnet has been shown to generalize seamlessly to much larger systems, such as polycyclic aromatics and semiconducting polymers, where even single-point CCSD(T) calculations are impossible.
Ultimately, the true impact of a universal DHNN will be measured by its seamless integration into end-to-end application workflows from quantum-transport and optical-response simulations to high-throughput materials screening. Realizing this vision demands the development of robust, modular interfaces and pipelines that permit straightforward fine-tuning and deployment of pretrained Hamiltonians across diverse computational tasks. By assembling such an interoperable software ecosystem, we can democratize access to first-principles accuracy and unlock new avenues for rapid, large-scale quantum mechanical discovery across the materials science community.
Deep Hamiltonian model for physical interpretation
DHNNs have rapidly established themselves as a transformative AI paradigm for materials discovery, achieving near-DFT accuracy across a spectrum of phenomena from MD and electron-phonon coupling (EPC) to quantum many-body interactions. By learning directly from high-fidelity training data and embedding core physical laws into their architectures, DHNNs offer a unified, data-driven alternative to conventional simulation workflows. Nevertheless, despite their outstanding predictive performance, these models remain largely “black boxes” with limited transparency into the mechanistic features driving their outputs. This opacity poses a significant barrier to scientific insight. Without interpretable representations of the learned Hamiltonian landscape, it is challenging to extract the underlying physics or to validate model predictions against established theoretical frameworks. Enhancing the interpretability of DHNNs is therefore essential to harness their full potential as tools for both prediction and discovery.
In contrast to the black-box nature often associated with deep learning, including DHNNs, traditional computational methods in physics, such as DFT, have long provided a framework for understanding physical phenomena through interpretable quantities. Recent advancements in the explainable GNNs offer a potential approach for the interpretability. GNN explainability methods, focusing on identifying the importance of nodes and edges within graph-structured data, have shown promise in attributing model predictions to specific structural features[93]. For instance, the ability to assign scientific meaning to nodes representing atoms and edges representing bonds in molecular graphs, as demonstrated in GNN explainer frameworks LRI and SubMT, highlights the potential to connect model interpretations to real-world scientific concepts[94,95]. Beyond GNNs, variational autoencoders (VAEs) offer a complementary path to interpretability for deep learning in physics. Visualizing VAE latent spaces, for example, via t-SNE, reveals physically meaningful representations learned in an unsupervised manner. Smooth trajectories and clustering in latent space, reflecting physical properties such as wavefunction smoothness and material similarity, demonstrate that VAEs can autonomously encode interpretable physical information[96]. This approach provides a crucial step towards bridging the interpretability gap in DHNNs, moving beyond “black box” predictions to deeper physical understanding.
Therefore, a crucial next step in the development of DHNNs lies in enhancing their explainability, moving beyond mere accuracy towards models that offer genuine scientific understanding, for example integrating interpretability techniques with DHNNs[97]. Exploring methods to map the learned Hamiltonian and its associated energy landscape within a DHNN to a graph representation, where nodes and edges could represent physical entities and interactions, could enable the application of GNN explainability tools. This could potentially reveal which physical components or interactions within the Hamiltonian learned by the DHNN are most salient for predicting specific physical phenomena. Furthermore, investigating the gradients of the DHNN’s energy function with respect to input features, and visualizing these gradients on a graph representation of the system, may unveil crucial physical insights driving the model’s predictions. Future research should prioritize the development of methods that integrate the predictive power of DHNNs with the interpretable scientific models. By fostering the creation of truly explainable DHNNs, we can unlock their full potential to accelerate scientific discovery, providing not only accurate simulations but also transparent and insightful tools for advancing our understanding of the physical world.
Applications in complex physical systems
Early applications of DHNNs have already demonstrated dramatic acceleration in electronic structure calculations while achieving the accuracy of conventional DFT for key observables such as band-structure predictions [Figure 4]. However, these proof-of-principle results represent only the first step. DHNNs are now poised to move beyond benchmark systems and tackle a host of more demanding application-driven challenges, for example non-adiabatic excited-state dynamics, complex magnetic phases, large-scale quantum transport [Figure 4B]. Thus, it can push the frontiers of computational materials modeling into new regimes of scale and physical complexity.
One significant frontier lies in the field of magnetic materials. Magnetic superstructures, including phenomena such as altermagnets, magnetic skyrmions and spin-spiral magnets, are attracting immense interest due to their emergent quantum physics. However, investigating these complex magnetic phases traditionally with ab initio accuracy has been hampered by formidable computational costs. To surmount this bottleneck, an extended DFT Hamiltonian framework, termed xDeepH, has been developed. This framework integrates both atomic structures {R} and magnetic configurations {M}, while crucially adhering to the equivariance requirements dictated by Euclidean and time-reversal symmetries. This sophisticated architectural design is crucial in capturing the subtle magnetic effects that govern the spin dynamics of these materials, demonstrating a pioneering approach to magnetic materials research.
Beyond ground-state properties, DHNNs are making significant strides in simulating excited-state dynamics in solids. Non-adiabatic MD (NAMD) simulations are essential for understanding a wide range of excited-state phenomena, including the energy transfer processes in solar cells and ultrafast carrier dynamics in semiconductors. However, conventional DFT-based NAMD simulations are computationally demanding and often suffer from accuracy limitations associated with standard exchange-correlation functionals. Zhang et al. introduced N2AMD, a framework that leverages E(3)-equivariant deep neural Hamiltonians to address these challenges[98]. Validated on prototypical semiconductors of TiO2 and GaAs, N2AMD accurately simulates electron-hole recombination behavior at a hybrid functional level (HSE06). This framework hints at pathways to establish a more reliable and efficient paradigm for NAMD simulations in complex condensed matter systems.
The ability of DHNNs to accelerate the density functional perturbation theory (DFPT) calculations represents another pivotal advancement. Perturbation responses are fundamental to understanding a vast spectrum of material properties, including temperature-dependent band gaps, non-radiative carrier recombination, and electron-phonon driven phenomena such as thermal and electrical conductivity and superconductivity. Deep learning frameworks, such as HamGNN and DeepH, are now being deployed to streamline EPC calculations. These models achieve acceleration by training neural networks to predict key quantities such as the Kohn-Sham potential or Hamiltonian matrix from DFT data of (perturbed) atomic structures. The computationally expensive derivatives with respect to atomic displacements, crucial for DFPT, are then efficiently obtained via automatic differentiation of the neural network[79] or by differentiating the network’s Hamiltonian predictions[85]. This circumvents the need to solve the costly Sternheimer equations for each perturbation mode, which is the bottleneck in traditional DFPT. These models provide an efficient toolkit for investigating diverse EPC-related phenomena, enabling calculations for large-scale systems with advanced functionals under perturbation, which were previously computationally prohibitive. Furthermore, the success of DHNNs in DFPT for EPC calculations opens exciting possibilities for generalizing these frameworks to investigate other types of perturbations, such as strain and external fields.
Meanwhile, the realm of quantum transport in nanoelectronics is being revolutionized by DHNNs. Simulating electron transport in nanoscale devices, particularly using the non-equilibrium Green’s function (NEGF) method, is computationally intensive, hindering the design and optimization of advanced nano-electronic components[99]. Zou et al. presented the DeePTB-NEGF[64], a novel deep learning framework that resolves this efficiency challenge. By integrating the DeePTB Hamiltonian approach with the NEGF method, DeePTB-NEGF achieves first-principles accuracy while circumventing the computationally expensive SCF iterations inherent in traditional DFT-NEGF methods. Validated through comprehensive simulations of break junctions and carbon nanotube field-effect transistors (CNT-FETs), DeePTB-NEGF demonstrates excellent agreement with experimental results and offers a powerful, high-throughput approach for simulating quantum transport across diverse nano-electronic devices.
Although significant progress has been made in above mentioned complex physics scenario, there are many complex physical systems for DHNNs, such as non-collinear magnets, topological quantum materials, high-order anharmonic phonon interactions, superconductivity, amorphous structures and more. In non-collinear antiferromagnets, DHNNs could improve the precision of modeling spin interactions and magnetic phase transitions by efficiently capturing the underlying energy landscapes[100]. Similarly, in topological materials, these networks are expected to reveal nuanced insights into the interplay between topology and electron dynamics, thereby supporting the design of quantum devices and spintronic applications[101]. Moreover, when dealing with complex electron-phonon interaction on thermoelectric properties[102], DHNNs have the potential to elucidate phonon behavior and energy dissipation mechanisms at multiple scales, offering a robust alternative to traditional simulation methods. These frontier applications represent the next wave of DHNN innovation, building upon the established successes in electronic structure, magnetic materials, excited-state dynamics, and quantum transport.
CONCLUSION AND OUTLOOK
ML-IAPs for MD and machine-learning Hamiltonian for electronic structure calculations have shown significant promise in advancing materials simulations, offering near ab initio accuracy while enabling access to larger length and time scales. The development of SOTA deep learning models has enabled more accurate and efficient predictions of interatomic and electronic properties. These advancements are crucial for the study and design of new materials, addressing the limitations of traditional methods such as MD and DFT.
Despite the progress, several challenges remain. The accuracy of ML-IAPs is heavily dependent on the quality and quantity of training data, which necessitates comprehensive data-sharing initiatives and improved DFT calculations. Additionally, the computational demands of these models, especially for large-scale simulations, are significant. Incorporating physical constraints and leveraging active learning can enhance the performance of these models, but a balance between computational expense and accuracy must be struck. The future of ML-IAPs is promising, with several key areas for development. Enhancing the generality and accuracy of models through larger and more diverse training datasets is essential. The integration of physical constraints and the adoption of coarse-graining techniques can further improve the efficiency and applicability of these models. High parallel efficiency is another potential direction of ML in materials science.
DHNNs are promising tools for electronic structure prediction but face challenges in generalizing across diverse material systems and scaling to larger systems. Extending their applicability to encompass the entire periodic table remains an ongoing research endeavor. Beyond electronic structures, DHNNs hold potential in modeling complex physical systems such as non-collinear magnets, topological quantum materials, high-order anharmonic phonon interactions, and superconductivity. Enhancing the explainability of DHNNs is crucial for advancing scientific understanding, which could involve integrating interpretability techniques such as mapping learned Hamiltonians to graph representations. Future research should focus on combining the predictive power of DHNNs with interpretable scientific models to accelerate scientific discovery.
DECLARATIONS
Acknowledgments
The authors thank Dr. Ziduo Yang for his insightful discussions and valuable suggestions. We also thank Ying Zhang for her generously sharing and meticulously collecting literature, particularly related to machine-learned Hamiltonians. Additionally, we acknowledge computational resources and support provided by National University of Singapore.
Authors’ contributions
Conceived and designed this review: Shen, L.
Conducted the machine learning interatomic potentials section: Li, Y.
Conducted the machine learning Hamiltonian part: Zhang, X.; Liu, M.; Li, Y.
Drafted manuscript: Li, Y.; Zhang, X.; Liu, M.
Edited the manuscript: Shen, L.
All authors reviewed the results and approved the final version of the manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was supported by Singapore MOE Tier 1 (No. A-8001194-00-00) and Singapore MOE Tier 2 (No. A-8001872-00-00).
Conflicts of interest
Shen, L. is an Editorial Board Member of Journal of Materials Informatics but is not involved in any steps of editorial processing, notably including reviewer selection, manuscript handling, or decision-making, while the other authors have declared that they have no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Krishtal, A.; Sinha, D.; Genova, A.; Pavanello, M. Subsystem density-functional theory as an effective tool for modeling ground and excited states, their dynamics and many-body interactions. J. Phys. Condens. Matter. 2015, 27, 183202.
2. Kohn, W.; Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133-8.
3. Brockherde, F.; Vogt, L.; Li, L.; Tuckerman, M. E.; Burke, K.; Müller, K. R. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 2017, 8, 872.
4. Li, H.; Wang, Z.; Zou, N.; et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation. Nat. Comput. Sci. 2022, 2, 367-77.
5. Kochkov, D.; Pfaff, T.; Sanchez-Gonzalez, A.; Battaglia, P.; Clark, B. K. Learning ground states of quantum Hamiltonians with graph networks. arXiv 2021, arXiv:2110.16390. https://doi.org/10.48550/arXiv.2110.06390. (accessed 30 Jun 2025).
6. Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401.
7. Bartók, A. P.; Payne, M. C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403.
8. Zhang, L.; Han, J.; Wang, H.; Car, R.; E, W. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett. 2018, 120, 143001.
9. Chan, H.; Narayanan, B.; Cherukara, M. J.; et al. Machine learning classical interatomic potentials for molecular dynamics from first-principles training data. J. Phys. Chem. C. 2019, 123, 6941-57.
10. Ko, T. W.; Ong, S. P. Recent advances and outstanding challenges for machine learning interatomic potentials. Nat. Comput. Sci. 2023, 3, 998-1000.
11. Yang, Z.; Wang, X.; Li, Y.; Lv, Q.; Chen, C. Y.; Shen, L. Efficient equivariant model for machine learning interatomic potentials. npj. Comput. Mater. 2025, 11, 1535.
12. Ahmad, W.; Simon, E.; Chithrananda, S.; Grand, G.; Ramsundar, B. ChemBERTa-2: towards chemical foundation models. arXiv 2022, arXiv:2209.01712. https://doi.org/10.48550/arXiv.2209.01712. (accessed 30 Jun 2025).
13. Li, J.; Jiang, X.; Wang, Y. Mol‐BERT: an effective molecular representation with BERT for molecular property prediction. Wirel. Commun. Mob. Comput. 2021, 2021, 7181815.
14. Batzner, S.; Musaelian, A.; Sun, L.; et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 2022, 13, 2453.
15. Duignan, T. T. The potential of neural network potentials. ACS. Phys. Chem. Au. 2024, 4, 232-41.
16. Dong, L.; Zhang, X.; Yang, Z.; Shen, L.; Lu, Y. Accurate piezoelectric tensor prediction with equivariant attention tensor graph neural network. npj. Comput. Mater. 2025, 11, 1546.
17. Zitnick, C. L.; Das, A.; Kolluru, A.; et al. Spherical channels for modeling atomic interactions. arXiv 2022, arXiv:2206.14331. https://doi.org/10.48550/arXiv.2206.14331. (accessed 30 Jun 2025).
18. Frank, J. T.; Unke, O. T.; Müller, K. R.; Chmiela, S. A Euclidean transformer for fast and stable machine learned force fields. Nat. Commun. 2024, 15, 6539.
19. Yuan, Z.; Xu, Z.; Li, H.; et al. Equivariant neural network force fields for magnetic materials. Quantum. Front. 2024, 3, 55.
20. Yu, H.; Zhong, Y.; Hong, L.; et al. Spin-dependent graph neural network potential for magnetic materials. Phys. Rev. B. 2024, 109, 144426.
21. Wang, H.; Zhang, L.; Han, J.; E, W. DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178-84.
22. Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Buchelnikov, V. Meta-GGA SCAN functional in the prediction of ground state properties of magnetic materials: review of the current state. Metals 2023, 13, 728.
23. Kirklin, S.; Saal, J. E.; Meredig, B.; et al. The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. npj. Comput. Mater. 2015, 1, BFnpjcompumats201510.
24. Ramakrishnan, R.; Dral, P. O.; Rupp, M.; von, Lilienfeld. O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data. 2014, 1, 140022.
25. Chmiela, S.; Tkatchenko, A.; Sauceda, H. E.; Poltavsky, I.; Schütt, K. T.; Müller, K. R. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 2017, 3, e1603015.
26. Chmiela, S.; Vassilev-Galindo, V.; Unke, O. T.; et al. Accurate global machine learning force fields for molecules with hundreds of atoms. arXiv 2022, arXiv 2209.14865. https://doi.org/10.48550/arXiv.2209.14865. (accessed 30 Jun 2025).
27. Smith, J. S.; Isayev, O.; Roitberg, A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192-203.
28. Smith, J. S.; Nebgen, B.; Lubbers, N.; Isayev, O.; Roitberg, A. E. Less is more: sampling chemical space with active learning. J. Chem. Phys. 2018, 148, 241733.
29. Smith, J. S.; Nebgen, B. T.; Zubatyuk, R.; et al. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903.
30. Devereux, C.; Smith, J. S.; Huddleston, K. K.; et al. Extending the applicability of the ANI Deep learning molecular potential to sulfur and halogens. J. Chem. Theory. Comput. 2020, 16, 4192-202.
31. Schütt, K. T.; Sauceda, H. E.; Kindermans, P. J.; Tkatchenko, A.; Müller, K. R. SchNet - a deep learning architecture for molecules and materials. J. Chem. Phys. 2018, 148, 241722.
32. Eastman, P.; Behara, P. K.; Dotson, D. L.; et al. SPICE, a dataset of drug-like molecules and peptides for training machine learning potentials. Sci. Data. 2023, 10, 11.
33. Chanussot, L.; Das, A.; Goyal, S.; et al. Open Catalyst 2020 (OC20) dataset and community challenges. ACS. Catal. 2021, 11, 6059-72.
34. Tran, R.; Lan, J.; Shuaibi, M.; et al. The Open Catalyst 2022 (OC22) Dataset and Challenges for Oxide Electrocatalysts. ACS. Catal. 2023, 13, 3066-84.
35. Jain, A.; Ong, S. P.; Hautier, G.; et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL. Mater. 2013, 1, 011002.
36. Dunn, A.; Wang, Q.; Ganose, A.; Dopp, D.; Jain, A. Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm. npj. Comput. Mater. 2020, 6, 138.
37. Bursch, M.; Mewes, J. M.; Hansen, A.; Grimme, S. Best-practice DFT protocols for basic molecular computational chemistry. Angew. Chem. Int. Ed. Engl. 2022, 61, e202205735.
38. Ko, T. W.; Ong, S. P. Data-efficient construction of high-fidelity graph deep learning interatomic potentials. npj. Comput. Mater. 2025, 11, 1550.
39. Batatia, I.; Batzner, S.; Kovács, D. P.; et al. The design space of E(3)-equivariant atom-centred interatomic potentials. Nat. Mach. Intell. 2025, 7, 56-67.
40. Fu, X.; Wood, B. M.; Barroso-Luque, L.; et al. Learning smooth and expressive interatomic potentials for physical property prediction. arXiv 2025, arXiv 2502,12147. https://doi.org/10.48550/arXiv.2502.12147. (accessed 30 Jun 2025).
41. Chmiela, S.; Sauceda, H. E.; Müller, K. R.; Tkatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887.
42. Choudhary, K.; Congo, F. Y.; Liang, T.; Becker, C.; Hennig, R. G.; Tavazza, F. Evaluation and comparison of classical interatomic potentials through a user-friendly interactive web-interface. Sci. Data. 2017, 4, 160125.
43. Wilkinson, M. D.; Dumontier, M.; Aalbersberg, I. J.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data. 2016, 3, 160018.
44. Blaiszik, B.; Chard, K.; Pruyne, J.; Ananthakrishnan, R.; Tuecke, S.; Foster, I. The materials data facility: data services to advance materials science research. JOM 2016, 68, 2045-52.
45. Varughese, B.; Manna, S.; Loeffler, T. D.; Batra, R.; Cherukara, M. J.; Sankaranarayanan, S. K. R. S. Active and transfer learning of high-dimensional neural network potentials for transition metals. ACS. Appl. Mater. Interfaces. 2024, 16, 20681-92.
46. Zhang, L.; Lin, D. Y.; Wang, H.; Car, R.; E, W. Active learning of uniformly accurate interatomic potentials for materials simulation. Phys. Rev. Mater. 2019, 3, 023804.
47. Zhang, L.; Chen, Z.; Su, J.; Li, J. Data mining new energy materials from structure databases. Renew. Sust. Energy. Rev. 2019, 107, 554-67.
48. Focassio, B.; Freitas, L. P. M.; Schleder, G. R. Performance assessment of universal machine learning interatomic potentials: challenges and directions for materials’ surfaces. ACS. Appl. Mater. Interfaces. 2025, 17, 13111-21.
49. Kim, Y.; Kim, Y.; Yang, C.; Park, K.; Gu, G. X.; Ryu, S. Deep learning framework for material design space exploration using active transfer learning and data augmentation. npj. Comput. Mater. 2021, 7, 609.
50. Mosquera-Lois, I.; Kavanagh, S. R.; Ganose, A. M.; Walsh, A. Machine-learning structural reconstructions for accelerated point defect calculations. npj. Comput. Mater. 2024, 10, 1303.
51. Omee, S. S.; Fu, N.; Dong, R.; Hu, M.; Hu, J. Structure-based out-of-distribution (OOD) materials property prediction: a benchmark study. npj. Comput. Mater. 2024, 10, 1316.
52. Musaelian, A.; Batzner, S.; Johansson, A.; et al. Learning local equivariant representations for large-scale atomistic dynamics. Nat. Commun. 2023, 14, 579.
53. Ma, X.; Chen, H.; He, R.; et al. Active learning of effective Hamiltonian for super-large-scale atomic structures. npj. Comput. Mater. 2025, 11, 1563.
54. Deng, B.; Zhong, P.; Jun, K.; et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 2023, 5, 1031-41.
55. Liao, Y. L.; Wood, B.; Das, A.; Smidt, T. EquiformerV2: improved equivariant transformer for scaling to higher-degree representations. arXiv 2023, arXiv:2306.12059. https://doi.org/10.48550/arXiv.2306.12059. (accessed 30 Jun 2025).
56. Riebesell, J.; Goodall, R. E. A.; Benner, P.; et al. Matbench discovery - a framework to evaluate machine learning crystal stability predictions. arXiv 2023, arXiv.2308.14920. https://doi.org/10.48550/arXiv.2308.14920. (accessed 30 Jun 2025).
57. Merchant, A.; Batzner, S.; Schoenholz, S. S.; Aykol, M.; Cheon, G.; Cubuk, E. D. Scaling deep learning for materials discovery. Nature 2023, 624, 80-5.
58. McClean, J. R.; Rubin, N. C.; Lee, J.; et al. What the foundations of quantum computer science teach us about chemistry. J. Chem. Phys. 2021, 155, 150901.
60. Allen, A. E. A.; Lubbers, N.; Matin, S.; et al. Learning together: towards foundation models for machine learning interatomic potentials with meta-learning. npj. Comput. Mater. 2024, 10, 1339.
61. Zhong, Y.; Yu, H.; Yang, J.; Guo, X.; Xiang, H.; Gong, X. Universal machine learning Kohn–Sham Hamiltonian for materials. Chinese. Phys. Lett. 2024, 41, 077103.
62. Curchod, B. F. E.; Martínez, T. J. Ab initio nonadiabatic quantum molecular dynamics. Chem. Rev. 2018, 118, 3305-36.
63. Babadi, M.; Knap, M.; Martin, I.; Refael, G.; Demler, E. Theory of parametrically amplified electron-phonon superconductivity. Phys. Rev. B. 2017, 96, 014512.
64. Zou, J.; Zhouyin, Z.; Lin, D.; Zhang, L.; Hou, S.; Gu, Q. Deep learning accelerated quantum transport simulations in nanoelectronics: from break junctions to field-effect transistors. arXiv 2024, arXiv:2411.08800. https://doi.org/10.48550/arXiv.2411.08800. (accessed 30 Jun 2025).
65. Yan, B. Spin-orbit coupling: a relativistic effect. 2016. https://tms16.sciencesconf.org/data/pages/SOC_lecture1.pdf. (accessed 30 Jun 2025).
66. Inorganic Chemistry II review: 6.1 solid state structures. https://library.fiveable.me/inorganic-chemistry-ii/unit-6/solid-state-structures/study-guide/qnl67GdXxyZ74VJP. (accessed 30 Jun 2025).
67. Gong, X.; Li, H.; Zou, N.; Xu, R.; Duan, W.; Xu, Y. General framework for E(3)-equivariant neural network representation of density functional theory Hamiltonian. Nat. Commun. 2023, 14, 2848.
68. Schütt, K. T.; Gastegger, M.; Tkatchenko, A.; Müller, K. R.; Maurer, R. J. Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions. Nat. Commun. 2019, 10, 5024.
69. Unke, O. T.; Bogojeski, M.; Gastegger, M.; Geiger, M.; Smidt, T.; Muller, K. R. SE(3)-equivariant prediction of molecular wavefunctions and electronic densities. In Advances in Neural Information Processing Systems 34 (NeurIPS 2021). 2021. https://proceedings.neurips.cc/paper/2021/hash/78f1893678afbeaa90b1fa01b9cfb860-Abstract.html. (accessed 30 Jun 2025).
70. Thomas, N.; Smidt, T.; Kearnes, S.; et al. Tensor field networks: rotation- and translation-equivariant neural networks for 3D point clouds. arXiv 2018, arXiv:1802.08219. https://doi.org/10.48550/arXiv.1802.08219. (accessed 30 Jun 2025).
71. Passaro, S.; Zitnick, C. L. Reducing SO(3) convolutions to SO(2) for efficient equivariant GNNs. arXiv 2023, arXiv:2302.03655. https://doi.org/10.48550/arXiv.2302.03655. (accessed 30 Jun 2025).
72. Wang, Y.; Li, H.; Tang, Z.; et al. DeepH-2: enhancing deep-learning electronic structure via an equivariant local-coordinate transformer. arXiv 2024, arXiv:2401.17015. https://doi.org/10.48550/arXiv.2401.17015. (accessed 30 Jun 2025).
73. Zhouyin, Z.; Gan, Z.; Liu, M.; Pandey, S. K.; Zhang, L.; Gu, Q. Learning local equivariant representations for quantum operators. arXiv 2024, arXiv:2407.06053. https://doi.org/10.48550/arXiv.2407.06053. (accessed 30 Jun 2025).
74. Li, Y.; Xia, Z.; Huang, L.; et al. Enhancing the scalability and applicability of Kohn-Sham Hamiltonians for molecular systems. arXiv 2025, arXiv:2502.19227. https://doi.org/10.48550/arXiv.2502.19227. (accessed 30 Jun 2025).
75. Yin, S.; Pan, X.; Wang, F.; He, L. TraceGrad: a framework learning expressive SO(3)-equivariant non-linear representations for electronic-structure Hamiltonian prediction. arXiv 2024, arXiv:2405.05722. https://doi.org/10.48550/arXiv.2405.05722. (accessed 30 Jun 2025).
76. Yu, H.; Xu, Z.; Qian, X.; Qian, X.; Ji, S. Efficient and equivariant graph networks for predicting quantum Hamiltonian. arXiv 2023, arXiv:2306.04922. https://doi.org/10.48550/arXiv.2306.04922. (accessed 30 Jun 2025).
77. Zhong, Y.; Yu, H.; Su, M.; Gong, X.; Xiang, H. Transferable equivariant graph neural networks for the Hamiltonians of molecules and solids. npj. Comput. Mater. 2023, 9, 1130.
78. Tang, Z.; Li, H.; Lin, P.; et al. A deep equivariant neural network approach for efficient hybrid density functional calculations. Nat. Commun. 2024, 15, 8815.
79. Li, H.; Tang, Z.; Fu, J.; et al. Deep-learning density functional perturbation theory. Phys. Rev. Lett. 2024, 132, 096401.
80. Yin, S.; Pan, X.; Zhu, X.; et al. Towards harmonization of SO(3)-equivariance and expressiveness: a hybrid deep learning framework for electronic-structure Hamiltonian prediction. Mach. Learn. Sci. Technol. 2024, 5, 045038.
81. Li, H.; Tang, Z.; Gong, X.; Zou, N.; Duan, W.; Xu, Y. Deep-learning electronic-structure calculation of magnetic superstructures. Nat. Comput. Sci. 2023, 3, 321-7.
82. Gong, X.; Louie, S. G.; Duan, W.; Xu, Y. Generalizing deep learning electronic structure calculation to the plane-wave basis. Nat. Comput. Sci. 2024, 4, 752-60.
83. Wang, Y.; Li, Y.; Tang, Z.; et al. Universal materials model of deep-learning density functional theory Hamiltonian. Sci. Bull. 2024, 69, 2514-21.
84. Tang, H.; Xiao, B.; He, W.; et al. Approaching coupled-cluster accuracy for molecular electronic structures with multi-task learning. Nat. Comput. Sci. 2025, 5, 144-54.
85. Zhong, Y.; Liu, S.; Zhang, B.; et al. Accelerating the calculation of electron-phonon coupling strength with machine learning. Nat. Comput. Sci. 2024, 4, 615-25.
86. Ma, Y.; Yu, H.; Zhong, Y.; Chen, S.; Gong, X.; Xiang, H. Transferable machine learning approach for predicting electronic structures of charged defects. Appl. Phys. Lett. 2025, 126, 044103.
87. Gu, Q.; Zhouyin, Z.; Pandey, S. K.; Zhang, P.; Zhang, L.; E, W. Deep learning tight-binding approach for large-scale electronic simulations at finite temperatures with ab initio accuracy. Nat. Commun. 2024, 15, 6772.
88. Zheng, H.; Sivonxay, E.; Christensen, R.; et al. The ab initio non-crystalline structure database: empowering machine learning to decode diffusivity. npj. Comput. Mater. 2024, 10, 1469.
89. Huang, P.; Lukin, R.; Faleev, M.; et al. Unveiling the complex structure-property correlation of defects in 2D materials based on high throughput datasets. npj. 2D. Mater. Appl. 2023, 7, 369.
90. Zhou, Z.; Zhou, Y.; He, Q.; Ding, Z.; Li, F.; Yang, Y. Machine learning guided appraisal and exploration of phase design for high entropy alloys. npj. Comput. Mater. 2019, 5, 265.
91. Chen, Y.; Zhang, L.; Wang, H.; E, W. DeePKS: a comprehensive data-driven approach toward chemically accurate density functional theory. J. Chem. Theory. Comput. 2021, 17, 170-81.
92. Ou, Q.; Tuo, P.; Li, W.; Wang, X.; Chen, Y.; Zhang, L. DeePKS model for halide perovskites with the accuracy of a hybrid functional. J. Phys. Chem. C. 2023, 127, 18755-64.
93. Kakkad, J.; Jannu, J.; Sharma, K.; Aggarwal, C.; Medya, S. A survey on explainability of graph neural networks. arXiv 2023, arXiv:2306.01958. https://doi.org/10.48550/arXiv.2306.01958. (accessed 30 Jun 2025).
94. Chen, Y.; Bian, Y.; Han, B.; Cheng, J. Interpretable and generalizable graph neural networks via subgraph multilinear extension. 2024. https://openreview.net/forum?id=dVq2StlcnY. (accessed 30 Jun 2025).
95. Miao, S.; Liu, M.; Li, P. Interpretable and generalizable graph learning via stochastic attention mechanism. arXiv 2022, arXiv 2201.12987. https://doi.org/10.48550/arXiv.2201.12987. (accessed 30 Jun 2025).
96. Hou, B.; Wu, J.; Qiu, D. Y. Unsupervised representation learning of Kohn-Sham states and consequences for downstream predictions of many-body effects. Nat. Commun. 2024, 15, 9481.
97. Miao, S.; Luo, Y.; Liu, M.; Li, P. Interpretable geometric deep learning via learnable randomness injection. arXiv 2022, arXiv 2210.16966. https://doi.org/10.48550/arXiv.2210.16966. (accessed 30 Jun 2025).
98. Zhang, C.; Tang, Z.; Zhong, Y.; Zou, N.; Tao, Z. G.; et al. Advancing nonadiabatic molecular dynamics simulations in solids with E(3) equivariant deep neural hamiltonians. Nat. Commun. 2025, 16, 2033.
99. Zhang, X.; Xu, L.; Lu, J.; Zhang, Z.; Shen, L. Physics-integrated neural network for quantum transport prediction of field-effect transistor. arXiv 2024, arXiv 2408.17023. https://doi.org/10.48550/arXiv.2408.17023. (accessed 30 Jun 2025).
100. Chen, X.; Liu, Y.; Liu, P.; et al. Unconventional magnons in collinear magnets dictated by spin space groups. Nature 2025, 640, 349-54.
101. Törmä, P.; Peotta, S.; Bernevig, B. A. Superconductivity, superfluidity and quantum geometry in twisted multilayer systems. Nat. Rev. Phys. 2022, 4, 528-42.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Issue
Copyright
Data & Comments
Data

















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.